The CAPD library provides mechanisms for easy computation of Poincare maps their derivatives. In general the Poincare map is defined by specifying

an ODE solver (instance of DOdeSolver, LDOdeSolver or IOdeSolver)
a function 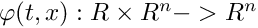$\alpha:R^n\to R$ that defines Poincare section. It is assumed that the function 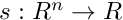$\alpha\in C^1$ is smooth and the Poincare section is given as
$\Pi = \{x\in R^n : \alpha(x) =0 \}$

In the CAPD a Poincare map is seen as a function

$P: R^n\to \Pi \subset R^n$

rather than a mapping from section to section. Initial point does not need to be on Poincare section 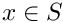$\Pi$ . We can compute intersection point of any trajectory with Poincare section.

We will give an overview on Poincare maps for both cases of rigorous and nonrigorous computations as they differ in details.

Poincare section is an object of class that implements interface defined in class AbstractSection. For user convenience we defined three classes that implement interface AbstractSection. Clearly the user can implement own class if necessary.

CoordinateSection - the section is given as 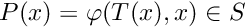$\alpha(x)=x_i-c$ for some index 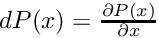and $c\in R$ .
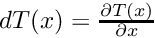AffineSection - the section is an affine hyperplane defined by normal vector and translation 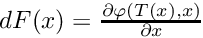$\alpha(x)=\langle n;x-c\rangle$ . We strongly recommend usage of affine sections that are locally orthogonal to the vector field.
NonlinearSection - the section is defined as arbitrary (possible nonlinear) map 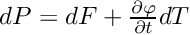$\alpha:R^n\to R$ . Constructors of this class have exactly the same arguments as of the class Function. In fact class NonlinearSection is derived from class Function.

For user convenience we defined the following types for computation in double D, long double LD, multiple precision Mp and in interval arithmetics I, MpI

DCoordinateSection, LDCoordinateSection, MpCoordinateSection, ICoordinateSection, MpICoordinateSection
DAffineSection, LDAffineSection, MpAffineSection, IAffineSection, MpIAffineSection
DNonlinearSection, LDNonlinearSection, MpNonlinearSection, INonlinearSection, MpINonlinearSection

In the examples below we will show how to use each of these types of Poincare sections. Thus, we will use type NonlinearSection even if the section will be linear - just to demonstrate how to define it.

Defining Poincare maps

Given an ODE solver (see section ODEs - nonrigorous methods)

int order = ...;
DMap vectorField(...);
DOdeSolver solver (vectorField,order);

and Poincare section

DCoordinateSection section(...);
// or DNonlinearSection section(...);
// or DAffineSection section(...);

we define an instance of Poincare map by constructor call

DPoincareMap pm(solver,section,crossingDirection);

The last argument specifies crossing direction of Poincare section. This is an enumeration type with three possible values

capd::poincare::MinusPlus - the function 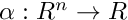$\alpha$ changes sign from minus to plus along trajectory
capd::poincare::PlusMinus - the function 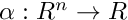$\alpha$ changes sign from plus to minus along trajectory
capd::poincare::Both - both directions are acceptable

Note: The argument crossingDirection of the constructor can be skipped. Its default value is capd::poincare::Both.

In similar way one can define an instance of IPoincareMap for rigorous computation of Poincare maps.

IMap vectorField("var:x,y;fun:-y,x;");
IOdeSolver solver(vectorField,20);
INonlinearSection section("var:x,y;fun:x;");
IPoincareMap pm (solver,section);

Attention: The objects vectorField, solver, section must exists during usage of object pm as pm holds references to them. In particular this code is incorrect
// do not use this in your code!

// Using object returned by this function can cause segmentation fault error.

DPoincareMap& createPoincareMap(){

DMap vectorField("var:x,y;fun:-y,x;");

DOdeSolver solver(vectorField,20);

DFunction section("var:x,y;fun:x;");

return *(new DPoincareMap(solver,section));

}

Instead one can define a little class for storing all objects (recommended)
struct MyPoincareMap{

MyPoincareMap(int order)

: vectorField(...),

solver(vectorField,order),

section(...),

pm(solver,section)

{}

DMap vectorField;

DOdeSolver solver;

DAffineSection section;

DPoincareMap pm;

};