Poincare map and return time - nonrigorous version

Given an instance of class PoincareMap one can compute image of a vector under Poincare map by call to overloaded operator

DPoincareMap pm(...);
DVector x(...);
double returnTime = 0; // must be initialized!
cout << "P(x)=" << pm(x,returnTime) << endl;
cout << "return time = " << returnTime << endl; 

Attention

The second argument returnTime must be initialized as it is used both as input and output parameter.

For autonomous systems it is usually initialized with zero. Then on output it will contain return time.
For nonautonomous systems its initial value specifies initial time for integration. On output it will contain the time at which intersection with Poincare section occurred.

Note: The second argument initialTime of the operator can be skipped - then the initial time for integration is set to zero by default.
DPoincareMap pm(...);

DVector x(...);

cout << "P(x)=" << pm(x) << endl;

Complete example (from examples/poincare/DPoincareMapExample.cpp):

#include <iostream>
#include "capd/capdlib.h"
 
using namespace std;
using namespace capd;
 
int main(){
  cout.precision(17);
 
  // Define vector field for the Lorenz system
  DMap lorenz("par:s,r,q;var:x,y,z;fun:s*(y-x),x*(r-z)-y,x*y-q*z;");
  lorenz.setParameter("s",10.);
  lorenz.setParameter("r",28.);
  lorenz.setParameter("q",8./3.);
 
  // Define solver
  DOdeSolver solver(lorenz,20);
 
  // Define Poincare section
  DNonlinearSection section("par:r;var:x,y,z;fun:z-r+1;");
  section.setParameter("r",28);
 
  // Define Poincare Map
  DPoincareMap pm(solver,section,poincare::PlusMinus);
 
  double returnTime=0;
 
  // Initial condition close to a periodic orbit
  double data[] = {-2.1473674741633753,2.0780481172873415,27};
  DVector x(3,data);
 
  cout << "     x=" << x << endl;
  x = pm(x,returnTime);
  cout << "  P(x)=" << x << ", halfReturnTime=" << returnTime<< endl;
  x = pm(x,returnTime);
  cout << "P^2(x)=" << x << ", fullReturnTime=" << returnTime<< endl;
  return 0;
}
 
/* output:
     x={-2.1473674741633753,2.0780481172873415,27}
  P(x)={2.1473675875613338,-2.0780482713004851,27}, halfReturnTime=0.77932610853932338
P^2(x)={-2.1473677282179087,2.078048081555901,27}, fullReturnTime=1.5586522078971192
*/
 

Derivatives of Poincare maps

The class DPoincareMap provides an overloaded operator for computation of Poincare map and its derivative. In order to compute Poincare map and its derivative we have to

specify initial condition for the main equation

double t = ...;

DVector initPoint(...);
define matrix that will store monodromy matrix - this is derivative of the flow 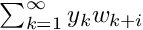$\phi(t,x)$ with respect to 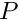and evaluated at 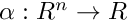equal to return time
DMatrix monodromyMatrix(...);
call operator that computes simultaneously Poincare map and monodromy matrix
DPoincareMap pm(...);

double returnTime = 0.; // must be initialized

DVector P = pm(initPoint,monodromyMatrix,returnTime);

Note
The last argument returnTime is optional and can be skipped for autonomous systems

After successful integration we have

P is an aproximate value of Poincare map at initPoint
approximate monodromy matrix monodromyMatrix

Given monodromy matrix we can recompute it to derivative of Poincare map by

DMatrix DP = pm.computeDP(P,monodromyMatrix,returnTime);

Note: for nonautonomous systems the argument returnTime can be skipped

Note: we split computation of derivative of Poincare map into computation of monodromy matrix and solving implicit equation. This is because the user can provide own and optimized routine for recomputation of monodromy matrix to derivative of Poincare map. For user convenience we provide a general routine computeDP.

Note: The matrix DP returned by computeDP is in full dimension. One can take a submatrix of DP that correspond to variables on the section.

Complete example (from examples/poincare/DPoincareMapDerivativeExample.cpp):

#include <iostream>
 
#include "capd/capdlib.h"
 
using namespace capd;
using namespace std;
 
// ----------------------------------- MAIN ----------------------------------------
 
int main()
{
  cout.precision(17);
  try{
    DMap vectorField("par:a,b;var:x,y,z;fun:-(y+z),x+b*y,b+z*(x-a);");
    vectorField.setParameter("a",5.7);
    vectorField.setParameter("b",0.2);
 
    DOdeSolver solver(vectorField,20);
 
    // MinusPlus means that the section is crossed with 'x' changing sign from minus to plus
    DCoordinateSection section(3,0); //  the section is x=0, 0-index from 3
    DPoincareMap pm(solver,section,poincare::MinusPlus);
 
    // this point is very close to fixed point for the Poincare map
    double data[] = {0.,-8.3809417428298 , 0.029590060630665};
    DVector u(3, data);
    double returnTime = 0.;
    DMatrix monodromyMatrix(3,3);
 
    // compute Poincare map
    DVector P = pm(u,monodromyMatrix,returnTime);
 
    // recompute monodromy matrix to derivative of Poincare map
    DMatrix DP = pm.computeDP(P,monodromyMatrix,returnTime);
 
    // print results
    cout << "   u=" << u << endl;
    cout << "P(u)=" << P << endl;
    cout << "return time = " << returnTime << endl;
    cout << "monodromyMatrix=" << monodromyMatrix << endl;
    cout << "DP(u)=" << DP << endl;
   }catch(exception& e)
  {
    cout << "\n\nException caught: "<< e.what() << endl;
  }
  return 0;
}
 
/* output:
   u={0,-8.3809417428297994,0.029590060630665001}
P(u)={-5.5511151231257827e-17,-8.3809417428300641,0.029590060630667017}
return time = 5.8810884555538996
monodromyMatrix={
{0.50685970275960168,-2.4490247655232884,0.4263784329575836},
{-0.59178625525395556,-1.9133051621539718,1.8817251176642307},
{0.0016796765683430427,-0.010279868615685349,0.0024919275429165304}
}
DP(u)={
{0,0,0},
{-0.49005513908815546,-2.404845565855263,1.9673029484873146},
{-0.00022220565883626208,-0.0010904289144987797,0.00089203400377833864}
}
*/