Files | |
| file | PdeCoordinateSection.h |
| file | pointst.cpp |
Namespaces | |
| capd | |
Classes | |
| class | capd::poincare::AbstractSection< MatrixT > |
| PoicareSection is class that is default PoincareSection for class PoincareMap. More... | |
| class | capd::poincare::AffineSection< MatrixT > |
| TimeMap class provides class that serves as an affine Poincare section. More... | |
| class | capd::poincare::BasicPoincareMap< SolverT, SectionT > |
| BasicPoicareMap class is mainly used for non-rigorous computations of Poincare Map. More... | |
| class | capd::poincare::CoordinateSection< MatrixT > |
| TimeMap class provides class that serves as Poincare section of the form x_i = c. More... | |
| class | capd::poincare::NonlinearSection< MatrixT > |
| TimeMap class provides class that serves as Poincare section of the form x_i = c. More... | |
| class | capd::poincare::PoincareException< setType > |
| class | capd::poincare::PoincareMap< SolverT, SectionT > |
| PoicareMap class rigorously computes Poincare Map. More... | |
| class | capd::poincare::SaveStepControl< DS > |
| it saves step and step control settings on construction and restores them on destruction. More... | |
| struct | capd::poincare::SectionDerivativesEnclosure< MatrixT > |
| class | capd::poincare::TimeMap< SolverT > |
| TimeMap class provides methods for transport of sets (or points) by a given flow over some time interval. More... | |
Enumerations | |
| enum | capd::poincare::CrossingDirection { capd::poincare::PlusMinus = 1, capd::poincare::Both = 0, capd::poincare::MinusPlus = -1 } |
| Defines constants to specify section crossing direction. More... | |
Functions | |
| void | initGraphics () |
| int | main (int, char *[]) |
| virtual void | capd::poincare::AbstractSection< MatrixT >::computeDT (const MatrixType &derivativeOfFlow, const VectorType &gradientOnPx, const ScalarType &denominator, VectorType &result) const |
| computes gradient of return time More... | |
| virtual MatrixType | capd::poincare::AbstractSection< MatrixT >::computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, const VectorType &fieldOnPx, VectorType &dT) const |
| Simultaneous computation of gradient of return time and derivative of Poincare Map dP. More... | |
| virtual void | capd::poincare::AbstractSection< MatrixT >::computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, const HessianType &hessianOfFlow, const VectorType &fieldOnPx, const VectorType &d2Phidt2, const MatrixType &derOfVectorFieldOnPx, MatrixType &DP, HessianType &D2P, VectorType &dT, MatrixType &d2T) const |
| Simultaneous computation of first and second Taylor coefficients of return time and Poincare map. More... | |
| capd::poincare::BasicPoincareMap< SolverT, SectionT >::BasicPoincareMap (Solver &solver, SectionType §ion, CrossingDirection direction=Both, const RealType &errorTolerance=pow(TypeTraits< RealType >::epsilon(), RealType(14.)/RealType(15.))) | |
| Constructor. More... | |
| ScalarType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::findRelativeCrossingTime (ScalarType timeJustBeforeSection, const CurveType &curve) |
This function computes time needed to cross the section from a point which is just before the section. Given 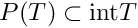 solves for solves for 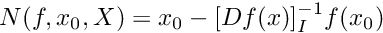 satisfying satisfying 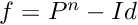 by a Newton like scheme. This is just scalar equation with one unknown. Then, computed return time is used to integrate the point by a Newton like scheme. This is just scalar equation with one unknown. Then, computed return time is used to integrate the point 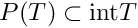 and compute Poincare map. More... and compute Poincare map. More... | |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, const HessianType &hessianOfFlow, MatrixType &DP, HessianType &D2P, VectorType &dT, MatrixType &d2T, ScalarType returnTime=TypeTraits< ScalarType >::zero()) |
| Simultaneous computation of first and second Taylor coefficients of return time and Poincare map. More... | |
| const Solver & | capd::poincare::BasicPoincareMap< SolverT, SectionT >::getSolver () const |
| Returns read-only reference to solver used to integrate the system. More... | |
| const Solver & | capd::poincare::BasicPoincareMap< SolverT, SectionT >::getDynamicalSystem () const |
| Returns read-only reference to solver used to integrate the system. More... | |
| VectorFieldType & | capd::poincare::BasicPoincareMap< SolverT, SectionT >::getVectorField () |
| Returns reference to solver used to integrate the system. More... | |
| const SectionType & | capd::poincare::BasicPoincareMap< SolverT, SectionT >::getSection () const |
| Returns reference to Poincare section object. More... | |
| size_type | capd::poincare::BasicPoincareMap< SolverT, SectionT >::getOrder () const |
| Returns order of numerical method used. More... | |
| ScalarType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::getStep () const |
| Returns time step. More... | |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::setOrder (size_type newOrder) |
| Sets order of Taylor method. More... | |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::setStep (const ScalarType &newStep) |
| Sets time step for integration of DS. More... | |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::setFactor (double newFactor) |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::setSection (const SectionType &newSection) |
| Sets new section function. More... | |
| MatrixType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, VectorType &dT, ScalarType returnTime=TypeTraits< ScalarType >::zero()) |
| Simultaneous computation of gradient of return time and derivative of Poincare Map dP. More... | |
| MatrixType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, ScalarType returnTime=TypeTraits< ScalarType >::zero()) |
| Computes derivative of Poincare Map dP. More... | |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, const HessianType &hessianOfFlow, MatrixType &DP, HessianType &D2P, ScalarType returnTime=TypeTraits< ScalarType >::zero()) |
| Simultaneous computation of first and second Taylor coefficients of return time and Poincare map. More... | |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::turnOnStepControl () |
| Disables automatic step control. More... | |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::turnOffStepControl () |
| Enables automatic step control. Step control strategy is built in the solver. More... | |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::onOffStepControl (bool sc) |
| Disables or enables automatic step control. More... | |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::setMaxReturnTime (double maxReturnTime) |
| Sets maximal return time to Poincare section. If the trajectory does not reach the section during time [0,maxReturnTime] then an exception is thrown. This prevents looping of the procedure computing Poincare map in the case when the trajectory is captured by an attractor (like sink or attracting periodic orbit) and never intersect Poincare section. More... | |
| void | capd::poincare::BasicPoincareMap< SolverT, SectionT >::setBlowUpMaxNorm (double blowUpMaxNorm) |
Sets threshold value of 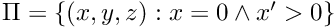 norm that is considered as a blow up of the solution. A trajectory may escape to infinity in finite time without crossing Poincare section. If the norm that is considered as a blow up of the solution. A trajectory may escape to infinity in finite time without crossing Poincare section. If the 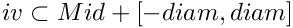 norm of a point on trajectory is bigger than this threshold value then an exception is thrown. More... norm of a point on trajectory is bigger than this threshold value then an exception is thrown. More... | |
| VectorType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() (const VectorType &v) |
| Computes value of Poincare Map. More... | |
| VectorType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() (VectorType v, ScalarType &in_out_time) |
| Computes value of Poincare Map. More... | |
| VectorType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() (VectorType v, VectorType &afterSection, ScalarType &in_out_time) |
| Computes value of Poincare Map. More... | |
| VectorType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() (const VectorType &v, MatrixType &dF) |
| Computes value of Poincare Map and derivativeof the flow. More... | |
| VectorType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() (VectorType v, MatrixType &dF, ScalarType &in_out_time) |
| Computes value of Poincare Map and derivative of the flow. More... | |
| VectorType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() (const VectorType &v, MatrixType &dF, HessianType &h) |
| Computes value of Poincare Map, derivative and hessian of the flow. More... | |
| VectorType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() (VectorType v, MatrixType &dF, HessianType &h, ScalarType &in_out_time) |
| Computes value of Poincare Map, derivative and hessian of the flow. More... | |
| VectorType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() (JetType &x) |
| Computes Poincare Map and derivatives of the flow to given order evaluated at return time. More... | |
| VectorType | capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() (JetType &x, ScalarType &in_out_time) |
| Computes Poincare Map and derivatives of the flow to given order evaluated at return time. More... | |
| template<typename T > | |
| T | capd::poincare::BasicPoincareMap< SolverT, SectionT >::integrateUntilSectionCrossing (T &x, int n=1, ScalarType *lastStep=0) |
Given an initial condition 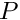 the function computes its trajetory until the function computes its trajetory until  -th intersection with the Poincare section. The point just before -th intersection with the Poincare section. The point just before 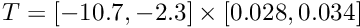 -th intersection is returned. More... -th intersection is returned. More... | |
| template<class JetT > | |
| JetT | capd::poincare::BasicPoincareMap< SolverT, SectionT >::computeDP (const JetT &DPhi) |
| Recomputes Taylor expansion of the flow into Taylor expansion of Poincare map. More... | |
| capd::poincare::PoincareMap< SolverT, SectionT >::PoincareMap (Solver &solver, SectionType §ion, CrossingDirection direction=Both, const BoundType &errorTolerance=0.1) | |
| Constructs PoincareMap for given dynamical system and section. More... | |
| template<typename T > | |
| ScalarType | capd::poincare::PoincareMap< SolverT, SectionT >::getSign (const T &theSet) |
| Function returns section sign. It also checks If we crossed section and returned in one step. In this case it throws an exception. More... | |
| template<typename T > | |
| ScalarType | capd::poincare::PoincareMap< SolverT, SectionT >::getSign (const T &theSet, VectorType &position, bool updatePosition, const VectorType &bounds) |
| Function returns section sign. It also checks If we crossed section and returned in one step. In this case it throws an exception. More... | |
| template<typename T > | |
| ScalarType | capd::poincare::PoincareMap< SolverT, SectionT >::getSign (const T &theSet, VectorType &position, bool updatePosition) |
| Function returns section sign. It also checks for possible crossing the section and returning in one step. In this case it throws an exception. More... | |
| template<typename T > | |
| void | capd::poincare::PoincareMap< SolverT, SectionT >::integrateUntilSectionCrossing (T &theSet, T &nextSet, int n=1) |
The function propagates the set of initial conditions 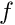 by the flow until its by the flow until its 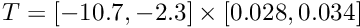 -th intersection with the Poincare section. More... -th intersection with the Poincare section. More... | |
| template<typename T > | |
| void | capd::poincare::PoincareMap< SolverT, SectionT >::getCloserToSection (T &theSet, T &nextSet) |
| On input: theSet is 'one step' before the section On output theSet is before the section and closer than sizeFactor*diam(theSet) in perpendicular direction to the section. More... | |
| template<typename T > | |
| bool | capd::poincare::PoincareMap< SolverT, SectionT >::crossSectionInOneStep (T &theSet, T &nextSet, ScalarType &oneStepReturnTime, VectorType &bound) |
| If it is possible to cross the section in one step, the function does this and returns bounf Computes return time by means of the Newton method. If not possible, returns false. More... | |
| template<typename T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::crossSection (T &theSet, T &nextSet) |
| Crosses the section and returns the value of Poincare Map. It updates also derivatives. We expect theSet to be just before the section. After this function theSet is on the section or just after the section. This function is common for all types of C^0, C^1, C^2 and C^n sets. More... | |
| template<typename T > | |
| void | capd::poincare::PoincareMap< SolverT, SectionT >::checkTransversability (const T &theSet, const VectorType &bounds) |
| Function checks if we crossed section and then returned in one step. In this case it throws an exception of PoincareException<T> type. More... | |
| template<class T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::computePoincareMap (T &originalSet, int n) |
| template<typename T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::operator() (T &theSet, const VectorType &x0, const MatrixType &A, ScalarType &out_returnTime, int n=1) |
| Computes value of n-th iterate of the Poincare Map. The result is returned in given affine coordinate system. More... | |
| template<typename T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::operator() (T &theSet, ScalarType &out_returnTime, int n=1) |
| Computes value of n-th iterate of the Poincare Map (used for C^0 sets) and returns bound of return time. More... | |
| template<typename T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::operator() (T &theSet, int n=1) |
| Computes value of n-th iterate of the Poincare Map (used for C^0 sets) More... | |
| template<typename T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::operator() (T &theSet, MatrixType &dF, ScalarType &out_returnTime, int n=1) |
| Computes value of n-th iterate of Poincare Map and derivatives of the flow (used for C^1 sets) More... | |
| template<typename T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::operator() (T &theSet, MatrixType &dF, int n=1) |
| Computes value of n-th iterate of Poincare Map and derivatives of the flow (used for C^1 sets) More... | |
| template<typename T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::operator() (T &theSet, MatrixType &dF, HessianType &hessian, ScalarType &out_returnTime, int n=1) |
| Computes value of n-th iterate of Poincare Map, derivatives and hessian of the flow (used for C^2 sets) More... | |
| template<typename T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::operator() (T &theSet, MatrixType &dF, HessianType &hessian, int n=1) |
| Computes value of n-th iterate of Poincare Map, derivatives and hessian of the flow (used for C^2 sets) More... | |
| template<typename T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::operator() (T &theSet, typename T::JetType &result, ScalarType &out_returnTime, int n=1) |
| Computes n-th iterate of Poincare Map and derivatives of the flow to given order (used for C^n sets) More... | |
| template<typename T > | |
| VectorType | capd::poincare::PoincareMap< SolverT, SectionT >::operator() (T &theSet, typename T::JetType &result, int n=1) |
| Computes n-th iterate of Poincare Map and derivatives of the flow to given order (used for C^n sets) More... | |
| void | capd::poincare::SectionDerivativesEnclosure< MatrixT >::updateEnclosure (C1Set &prev, C1Set &next) |
| void | capd::poincare::SectionDerivativesEnclosure< MatrixT >::updateEnclosure (C2Set &prev, C2Set &next) |
| void | capd::poincare::SectionDerivativesEnclosure< MatrixT >::updateEnclosure (CnSet &prev, CnSet &next) |
| capd::poincare::TimeMap< SolverT >::TimeMap (Solver &solver) | |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v) |
| For a vector v it computes its position after time time. More... | |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, ScalarType &in_out_time) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, SolutionCurve &solution) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, MatrixType &derivative) |
| For a vector v it computes its position after time 'time' and derivative with respect to initial conditions. More... | |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, MatrixType &derivative, ScalarType &in_out_time) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, MatrixType &derivative, SolutionCurve &solution) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, const MatrixType &initMatrix, MatrixType &derivative) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, const MatrixType &initMatrix, MatrixType &derivative, ScalarType &in_out_time) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, const MatrixType &initMatrix, MatrixType &derivative, SolutionCurve &solution) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, MatrixType &derivative, HessianType &hessian) |
| Operators for integration of second order variational equations. More... | |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, MatrixType &derivative, HessianType &hessian, ScalarType &in_out_time) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, MatrixType &derivative, HessianType &hessian, SolutionCurve &solution) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, const MatrixType &initMatrix, const HessianType &initHessian, MatrixType &derivative, HessianType &hessian) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, const MatrixType &initMatrix, const HessianType &initHessian, MatrixType &derivative, HessianType &hessian, ScalarType &in_out_time) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, const MatrixType &initMatrix, const HessianType &initHessian, MatrixType &derivative, HessianType &hessian, SolutionCurve &solution) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, JetType &jet) |
| For a vector v it computes its position after time 'time' and higher order derivatives with respect to initial conditions. More... | |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, JetType &jet, ScalarType &in_out_time) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, JetType &jet, SolutionCurve &solution) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, const JetType &initJet, JetType &jet) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, const JetType &initJet, JetType &jet, ScalarType &in_out_time) |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, const JetType &initJet, JetType &jet, SolutionCurve &solution) |
| const Solver & | capd::poincare::TimeMap< SolverT >::getDynamicalSystem () const |
| Returns read-only reference to solver used to integrate the system. More... | |
| const Solver & | capd::poincare::TimeMap< SolverT >::getSolver () const |
| Returns read-only reference to solver used to integrate the system. More... | |
| const VectorFieldType & | capd::poincare::TimeMap< SolverT >::getVectorField () const |
| Returns read-only reference to current vector field. More... | |
| size_type | capd::poincare::TimeMap< SolverT >::getOrder () const |
| Returns order of numerical method. More... | |
| void | capd::poincare::TimeMap< SolverT >::setOrder (size_type newOrder) |
| sets new order of numerical method More... | |
| ScalarType | capd::poincare::TimeMap< SolverT >::getStep () const |
| Returns step of numerical method (does make sense only when step control is disabled) More... | |
| void | capd::poincare::TimeMap< SolverT >::setStep (const ScalarType &newStep) |
| Sets step of numerical method (does make sense only when step control is disabled) More... | |
| void | capd::poincare::TimeMap< SolverT >::turnOnStepControl () |
| Disables automatic step control. More... | |
| void | capd::poincare::TimeMap< SolverT >::turnOffStepControl () |
| Enables automatic step control. Step control strategy is builded into the dynamical system. More... | |
| void | capd::poincare::TimeMap< SolverT >::onOffStepControl (bool sc) |
| Disables or enables automatic step control. More... | |
| void | capd::poincare::TimeMap< SolverT >::stopAfterStep (bool b) |
| For dense output. If true, integration procedure returns after each successful step. The computation can be then resumed - see examples. More... | |
| bool | capd::poincare::TimeMap< SolverT >::completed () const |
| For dense output. Returns true if the trajectory has been integrated to the requested time. More... | |
| const ScalarType & | capd::poincare::TimeMap< SolverT >::getCurrentTime () const |
| For dense output. Returns current time during integration. More... | |
| template<class SetType > | |
| void | capd::poincare::TimeMap< SolverT >::initComputations (SetType &originalSet, void *current) |
| template<class SetType > | |
| void | capd::poincare::TimeMap< SolverT >::moveSet (ScalarType time, SetType &originalSet, void *current) |
| template<typename SetType > | |
| SolverT::VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType Time, SetType &originalSet) |
| template<typename SetType > | |
| SolverT::VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType Time, SetType &originalSet, SolutionCurve &solution) |
| template<typename SetType > | |
| SolverT::VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType Time, SetType &originalSet, MatrixType &derivative) |
| template<class CnCoeffType > | |
| VectorType | capd::poincare::TimeMap< SolverT >::operator() (ScalarType time, VectorType &v, CnCoeffType &result) |
Variables | |
| double | minx = -2.2 |
| double | maxx = 1.6 |
| double | miny = -2.6 |
| double | maxy = 2. |
| Frame | fr |
| Frame | txt |
Detailed Description
Enumeration Type Documentation
◆ CrossingDirection
Defines constants to specify section crossing direction.
Section is given zeros of some scalar function. PlusMinus means that we want to cross section comming from positive values and going to negative ones (MinusPlus means opposite direction). Constant None means that we do not specify direction, both are allowed.
| Enumerator | |
|---|---|
| PlusMinus | |
| Both | |
| MinusPlus | |
Function Documentation
◆ BasicPoincareMap()
| capd::poincare::BasicPoincareMap< SolverT, SectionT >::BasicPoincareMap | ( | Solver & | solver, |
| SectionType & | section, | ||
| CrossingDirection | direction = Both, |
||
| const RealType & | errorTolerance = pow(TypeTraits<RealType>::epsilon(), RealType(14.)/RealType(15.)) |
||
| ) |
Constructor.
◆ checkTransversability()
|
protected |
Function checks if we crossed section and then returned in one step. In this case it throws an exception of PoincareException<T> type.
◆ completed()
|
inline |
For dense output. Returns true if the trajectory has been integrated to the requested time.
◆ computeDP() [1/7]
| JetT capd::poincare::BasicPoincareMap< SolverT, SectionT >::computeDP | ( | const JetT & | PhiSeries | ) |
Recomputes Taylor expansion of the flow into Taylor expansion of Poincare map.
Computes all partial derivatives of a Poincare map to an arbitrarily order.
- Parameters
-
[in] Px partial derivatives of the flow to a given order
- Remarks
- Computations are valid only for linear sections.
◆ computeDP() [2/7]
|
virtual |
Simultaneous computation of first and second Taylor coefficients of return time and Poincare map.
- Parameters
-
[in] Px - value of Poincare map [in] derivativeOfFlow - solution to first variational equation computed at return time [in] hessianOfFlow - solution to first variational equation computed at return time [in] fieldOnPx - vector field evaluated at (t(Px),Px) [out] DP - computed derivative of Poincare map [out] D2P - computed second order Taylor coefficients of Poincare map [out] dT - computed gradient of return time [out] d2T - computed second order Taylor coefficients of return time [in] returnTime - return time to the section
- Note
- all input and output parameters are Taylor coefficients, not derivatives!
◆ computeDP() [3/7]
|
inline |
Simultaneous computation of first and second Taylor coefficients of return time and Poincare map.
- Parameters
-
[in] Px - value of Poincare map [in] derivativeOfFlow - solution to first variational equation computed at return time [in] hessianOfFlow - solution to first variational equation computed at return time [out] DP - computed derivative of Poincare map [out] D2P - computed second order Taylor coefficients of Poincare map [in] returnTime - return time to the section
- Note
- all input and output parameters are Taylor coefficients, not derivatives!
- returnTime must be specified for nonautonomous flows only. Otherwise, default value 0 is valid.
◆ computeDP() [4/7]
| void capd::poincare::BasicPoincareMap< SolverT, SectionT >::computeDP | ( | const VectorType & | Px, |
| const MatrixType & | derivativeOfFlow, | ||
| const HessianType & | hessianOfFlow, | ||
| MatrixType & | DP, | ||
| HessianType & | D2P, | ||
| VectorType & | dT, | ||
| MatrixType & | d2T, | ||
| ScalarType | returnTime = TypeTraits<ScalarType>::zero() |
||
| ) |
Simultaneous computation of first and second Taylor coefficients of return time and Poincare map.
- Parameters
-
[in] Px - value of Poincare map [in] derivativeOfFlow - solution to first variational equation computed at return time [in] hessianOfFlow - solution to first variational equation computed at return time [out] DP - computed derivative of Poincare map [out] D2P - computed second order Taylor coefficients of Poincare map [out] dT - computed gradient of return time [out] d2T - computed second order Taylor coefficients of return time [in] returnTime - return time to the section
- Note
- all input and output parameters are Taylor coefficients, not derivatives!
- returnTime must be specified for nonautonomous flows only. Otherwise, default value 0 is valid.
◆ computeDP() [5/7]
|
virtual |
Simultaneous computation of gradient of return time and derivative of Poincare Map dP.
- Parameters
-
[in] Px - value of Poincare map [in] derivativeOfFlow - solution to first variational equation computed at return time [out] dT - computed gradient of return time [in] returnTime - enclosure of return time
- Note
- returnTime must be specified for nonautonomous flows only. Otherwise, default value 0 is valid.
◆ computeDP() [6/7]
|
inline |
Computes derivative of Poincare Map dP.
- Parameters
-
[in] Px - value of Poincare map [in] derivativeOfFlow - solution to first variational equation computed at return time
- Note
- returnTime must be specified for nonautonomous flows only. Otherwise, default value 0 is valid.
◆ computeDP() [7/7]
|
inline |
Simultaneous computation of gradient of return time and derivative of Poincare Map dP.
- Parameters
-
[in] Px - value of Poincare map [in] derivativeOfFlow - solution to first order variational equation computed at return time [out] dT - computed gradient of return time [in] returnTime - computed return time
- Note
- returnTime must be specified for nonautonomous flows only. Otherwise, default value 0 is valid.
◆ computeDT()
|
virtual |
computes gradient of return time
- Parameters
-
[in] derivativeOfFlow - solution to first variational equation computed at return time [in] gradientOnPx - gradient of function that defines Poincare section evaluated at Px [in] denominator - scalar product of vector field evaluated at Px and gradientOnPx [out] result - computed gradient of return time
◆ computePoincareMap()
|
protected |
◆ crossSection()
|
protected |
Crosses the section and returns the value of Poincare Map. It updates also derivatives. We expect theSet to be just before the section. After this function theSet is on the section or just after the section. This function is common for all types of C^0, C^1, C^2 and C^n sets.
Function used to cross the section for all types of sets.
- Parameters
-
[in,out] theSet set just before the section, on exit is equal to setAfterTheSection [in] nextSet set on the section or just after it
- Returns
- set that contains value of Poincare map for given set theSet
◆ crossSectionInOneStep()
|
protected |
If it is possible to cross the section in one step, the function does this and returns bounf Computes return time by means of the Newton method. If not possible, returns false.
Function used to cross the section for all types of sets.
- Parameters
-
[in] theSet set just before the section [out] oneStepReturnTime bound for the return time in relative to current time of theSet [out] bound bound for the intersection of the trajectories with Poincare section
- Returns
- true if succeed
◆ findRelativeCrossingTime()
|
protected |
This function computes time needed to cross the section from a point which is just before the section. Given 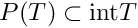 solves for
solves for 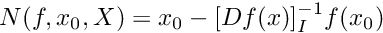 satisfying
satisfying 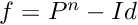 by a Newton like scheme. This is just scalar equation with one unknown. Then, computed return time is used to integrate the point
by a Newton like scheme. This is just scalar equation with one unknown. Then, computed return time is used to integrate the point 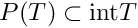 and compute Poincare map.
and compute Poincare map.
Crosses the section and returns the value of Poincare Map.
◆ getCloserToSection()
|
protected |
On input: theSet is 'one step' before the section On output theSet is before the section and closer than sizeFactor*diam(theSet) in perpendicular direction to the section.
*__________________________________________________________________________*/
◆ getCurrentTime()
|
inline |
For dense output. Returns current time during integration.
◆ getDynamicalSystem() [1/2]
|
inline |
Returns read-only reference to solver used to integrate the system.
◆ getDynamicalSystem() [2/2]
|
inline |
Returns read-only reference to solver used to integrate the system.
◆ getOrder() [1/2]
|
inline |
Returns order of numerical method.
◆ getOrder() [2/2]
|
inline |
Returns order of numerical method used.
◆ getSection()
|
inline |
Returns reference to Poincare section object.
◆ getSign() [1/3]
|
protected |
Function returns section sign. It also checks If we crossed section and returned in one step. In this case it throws an exception.
- Parameters
-
[in] theSet the set after making a step,
- Returns
- section sign evaluated on theSet
◆ getSign() [2/3]
|
protected |
Function returns section sign. It also checks for possible crossing the section and returning in one step. In this case it throws an exception.
- Parameters
-
[in] theSet the set after making a step, [in,out] position position before time step, [in] updatePosition flag that decided if position has to be updated
- Returns
- section sign
◆ getSign() [3/3]
|
protected |
Function returns section sign. It also checks If we crossed section and returned in one step. In this case it throws an exception.
- Parameters
-
[in] theSet the set after making a step, [in,out] position position before time step, [in] updatePosition flag that decides if position has to be updated [in] bound rough enclosure for trajectory during whole time step
- Returns
- section sign
◆ getSolver() [1/2]
|
inline |
Returns read-only reference to solver used to integrate the system.
◆ getSolver() [2/2]
|
inline |
Returns read-only reference to solver used to integrate the system.
◆ getStep() [1/2]
|
inline |
Returns step of numerical method (does make sense only when step control is disabled)
◆ getStep() [2/2]
|
inline |
Returns time step.
◆ getVectorField() [1/2]
|
inline |
Returns reference to solver used to integrate the system.
◆ getVectorField() [2/2]
|
inline |
Returns read-only reference to current vector field.
◆ initComputations()
|
protected |
◆ initGraphics()
| void initGraphics | ( | ) |
◆ integrateUntilSectionCrossing() [1/2]
|
protected |
The function propagates the set of initial conditions 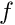 by the flow until its
by the flow until its 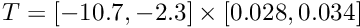 -th intersection with the Poincare section.
-th intersection with the Poincare section.
- Returns
- If succeed,
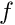 is one-integration-step close to the section and
is one-integration-step close to the section and 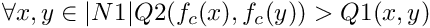 is either on the section or just after the section.
is either on the section or just after the section. -
true, if
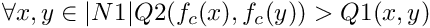 is after section and false, otherwise.
is after section and false, otherwise.
- Note
- : An exception is thrown if the solver cannot integrate the set
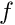 until its
until its 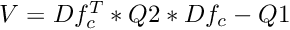 -th intersection with Poicnare section.
-th intersection with Poicnare section.
◆ integrateUntilSectionCrossing() [2/2]
|
protected |
Given an initial condition 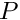 the function computes its trajetory until
the function computes its trajetory until 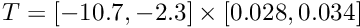 -th intersection with the Poincare section. The point just before
-th intersection with the Poincare section. The point just before 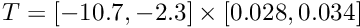 -th intersection is returned.
-th intersection is returned.
////////////////////////////////////////////////////////////////////////////////
- Note
- : An exception is thrown if either the maximal accepted return time is exceeded or the norm of a point on the trajectory exceeds maximal accpeted value. This may occur when the trajectory escapes to infinity.
- : An initial condition is a template parameter. It can be just a vector or a structure holding also intitial conditions for (higher order) variational equations.
This function moves theSet with the given flow and stops just before the section (for n-th iterate of Poincare Map).
- Returns
- set on the section or just after the section (suitable for a computation of next Poincare Map iteration).
Parameter theSet contains on return the set just before the section.
Common function for different set types. //////////////////////////////////////////////////////////////////////////////
@TODO : implement for n>1
- Parameters
-
theSet [in,out] theSet on input: initial set position, on return: the set just before the section. n number of iterates lastStep if given
◆ main()
◆ moveSet()
|
protected |
◆ onOffStepControl() [1/2]
|
inline |
Disables or enables automatic step control.
◆ onOffStepControl() [2/2]
|
inline |
Disables or enables automatic step control.
◆ operator()() [1/43]
| BasicPoincareMap< SolverT, FunT >::VectorType capd::poincare::BasicPoincareMap< SolverT, FunT >::operator() | ( | const VectorType & | v | ) |
Computes value of Poincare Map.
- Parameters
-
[in] v - argument of Poincare map
- Returns
- P(v) - first intersection of the trajectory of v with Poincare section.
◆ operator()() [2/43]
| BasicPoincareMap< SolverT, FunT >::VectorType capd::poincare::BasicPoincareMap< SolverT, FunT >::operator() | ( | const VectorType & | v, |
| MatrixType & | dF | ||
| ) |
Computes value of Poincare Map and derivativeof the flow.
- Parameters
-
[in] v - vector at which we want compute Poincare map [out] dF - derivative of the flow evaluated at (v,returnTime).
- Note
- This routine is valid for an autonomous flows, only.
◆ operator()() [3/43]
| BasicPoincareMap< SolverT, FunT >::VectorType capd::poincare::BasicPoincareMap< SolverT, FunT >::operator() | ( | const VectorType & | v, |
| MatrixType & | dF, | ||
| HessianType & | h | ||
| ) |
Computes value of Poincare Map, derivative and hessian of the flow.
- Parameters
-
[in] v - vector at which we want compute Poincare map [out] dF - derivative of the flow evaluated at (v,returnTime). [out] h - second order Taylor coefficients of flow evaluated at (v,returnTime).
- Note
- This routine is valid for an autonomous flows, only.
◆ operator()() [4/43]
| BasicPoincareMap< SolverT, SectionT >::VectorType capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() | ( | JetType & | x | ) |
Computes Poincare Map and derivatives of the flow to given order evaluated at return time.
Nonrigorous Poincare map.
This routine is valid for an autonomous flows, only.
A point just after the section on the nonrigorous trajectory is returned The result contains also approximate values of the partial derivatives of the flow
◆ operator()() [5/43]
| BasicPoincareMap< SolverT, SectionT >::VectorType capd::poincare::BasicPoincareMap< SolverT, SectionT >::operator() | ( | JetType & | x, |
| ScalarType & | in_out_time | ||
| ) |
Computes Poincare Map and derivatives of the flow to given order evaluated at return time.
Nonrigorous Poincare map.
This routine is valid for both autonomous and time-dependent vector fields.
A point just after the section on the nonrigorous trajectory is returned The result contains also approximate values of the partial derivatives of the flow
◆ operator()() [6/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| const JetType & | initJet, | ||
| JetType & | jet | ||
| ) |
◆ operator()() [7/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| const JetType & | initJet, | ||
| JetType & | jet, | ||
| ScalarType & | in_out_time | ||
| ) |
◆ operator()() [8/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| const JetType & | initJet, | ||
| JetType & | jet, | ||
| SolutionCurve & | solution | ||
| ) |
◆ operator()() [9/43]
| SolverT::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | Time, |
| SetType & | originalSet | ||
| ) |
◆ operator()() [10/43]
| SolverT::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | Time, |
| SetType & | originalSet, | ||
| MatrixType & | derivative | ||
| ) |
◆ operator()() [11/43]
| SolverT::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | Time, |
| SetType & | originalSet, | ||
| SolutionCurve & | solution | ||
| ) |
◆ operator()() [12/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v | ||
| ) |
For a vector v it computes its position after time time.
◆ operator()() [13/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| CnCoeffType & | result | ||
| ) |
◆ operator()() [14/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| const MatrixType & | initMatrix, | ||
| const HessianType & | initHessian, | ||
| MatrixType & | derivative, | ||
| HessianType & | hessian | ||
| ) |
◆ operator()() [15/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| const MatrixType & | initMatrix, | ||
| const HessianType & | initHessian, | ||
| MatrixType & | derivative, | ||
| HessianType & | hessian, | ||
| ScalarType & | in_out_time | ||
| ) |
◆ operator()() [16/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| const MatrixType & | initMatrix, | ||
| const HessianType & | initHessian, | ||
| MatrixType & | derivative, | ||
| HessianType & | hessian, | ||
| SolutionCurve & | solution | ||
| ) |
◆ operator()() [17/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| const MatrixType & | initMatrix, | ||
| MatrixType & | derivative | ||
| ) |
◆ operator()() [18/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| const MatrixType & | initMatrix, | ||
| MatrixType & | derivative, | ||
| ScalarType & | in_out_time | ||
| ) |
◆ operator()() [19/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| const MatrixType & | initMatrix, | ||
| MatrixType & | derivative, | ||
| SolutionCurve & | solution | ||
| ) |
◆ operator()() [20/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| JetType & | jet | ||
| ) |
For a vector v it computes its position after time 'time' and higher order derivatives with respect to initial conditions.
◆ operator()() [21/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| JetType & | jet, | ||
| ScalarType & | in_out_time | ||
| ) |
◆ operator()() [22/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| JetType & | jet, | ||
| SolutionCurve & | solution | ||
| ) |
◆ operator()() [23/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| MatrixType & | derivative | ||
| ) |
For a vector v it computes its position after time 'time' and derivative with respect to initial conditions.
◆ operator()() [24/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| MatrixType & | derivative, | ||
| HessianType & | hessian | ||
| ) |
Operators for integration of second order variational equations.
◆ operator()() [25/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| MatrixType & | derivative, | ||
| HessianType & | hessian, | ||
| ScalarType & | in_out_time | ||
| ) |
◆ operator()() [26/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| MatrixType & | derivative, | ||
| HessianType & | hessian, | ||
| SolutionCurve & | solution | ||
| ) |
◆ operator()() [27/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| MatrixType & | derivative, | ||
| ScalarType & | in_out_time | ||
| ) |
◆ operator()() [28/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| MatrixType & | derivative, | ||
| SolutionCurve & | solution | ||
| ) |
◆ operator()() [29/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| ScalarType & | in_out_time | ||
| ) |
◆ operator()() [30/43]
| TimeMap< SolverT >::VectorType capd::poincare::TimeMap< SolverT >::operator() | ( | ScalarType | time, |
| VectorType & | v, | ||
| SolutionCurve & | solution | ||
| ) |
◆ operator()() [31/43]
| PoincareMap< DS, FunT >::VectorType capd::poincare::PoincareMap< DS, FunT >::operator() | ( | T & | theSet, |
| const VectorType & | x0, | ||
| const MatrixType & | A, | ||
| ScalarType & | out_returnTime, | ||
| int | n = 1 |
||
| ) |
Computes value of n-th iterate of the Poincare Map. The result is returned in given affine coordinate system.
- Parameters
-
[in] theSet - set of initial conditions [in] x0 - origin of new coordinates [in] A - linear part of new coordinates [out] returnTime - bound for return time to the section [in] n - iterate of Poincare map to be computed
- Returns
- A*(P(theSet)-x0)
◆ operator()() [32/43]
| PoincareMap< DS, FunT >::VectorType capd::poincare::PoincareMap< DS, FunT >::operator() | ( | T & | theSet, |
| int | n = 1 |
||
| ) |
Computes value of n-th iterate of the Poincare Map (used for C^0 sets)
◆ operator()() [33/43]
| PoincareMap< DS, FunT >::VectorType capd::poincare::PoincareMap< DS, FunT >::operator() | ( | T & | theSet, |
| MatrixType & | dF, | ||
| HessianType & | hessian, | ||
| int | n = 1 |
||
| ) |
Computes value of n-th iterate of Poincare Map, derivatives and hessian of the flow (used for C^2 sets)
◆ operator()() [34/43]
| PoincareMap< DS, FunT >::VectorType capd::poincare::PoincareMap< DS, FunT >::operator() | ( | T & | theSet, |
| MatrixType & | dF, | ||
| HessianType & | hessian, | ||
| ScalarType & | out_returnTime, | ||
| int | n = 1 |
||
| ) |
Computes value of n-th iterate of Poincare Map, derivatives and hessian of the flow (used for C^2 sets)
◆ operator()() [35/43]
| PoincareMap< DS, FunT >::VectorType capd::poincare::PoincareMap< DS, FunT >::operator() | ( | T & | theSet, |
| MatrixType & | dF, | ||
| int | n = 1 |
||
| ) |
Computes value of n-th iterate of Poincare Map and derivatives of the flow (used for C^1 sets)
◆ operator()() [36/43]
| PoincareMap< DS, FunT >::VectorType capd::poincare::PoincareMap< DS, FunT >::operator() | ( | T & | theSet, |
| MatrixType & | dF, | ||
| ScalarType & | out_returnTime, | ||
| int | n = 1 |
||
| ) |
Computes value of n-th iterate of Poincare Map and derivatives of the flow (used for C^1 sets)
◆ operator()() [37/43]
| PoincareMap< DS, FunT >::VectorType capd::poincare::PoincareMap< DS, FunT >::operator() | ( | T & | theSet, |
| ScalarType & | out_returnTime, | ||
| int | n = 1 |
||
| ) |
Computes value of n-th iterate of the Poincare Map (used for C^0 sets) and returns bound of return time.
◆ operator()() [38/43]
| PoincareMap< DS, FunT >::VectorType capd::poincare::PoincareMap< DS, FunT >::operator() | ( | T & | theSet, |
| typename T::JetType & | result, | ||
| int | n = 1 |
||
| ) |
Computes n-th iterate of Poincare Map and derivatives of the flow to given order (used for C^n sets)
◆ operator()() [39/43]
| PoincareMap< DS, FunT >::VectorType capd::poincare::PoincareMap< DS, FunT >::operator() | ( | T & | theSet, |
| typename T::JetType & | result, | ||
| ScalarType & | out_returnTime, | ||
| int | n = 1 |
||
| ) |
Computes n-th iterate of Poincare Map and derivatives of the flow to given order (used for C^n sets)
◆ operator()() [40/43]
| BasicPoincareMap< SolverT, FunT >::VectorType capd::poincare::BasicPoincareMap< SolverT, FunT >::operator() | ( | VectorType | v, |
| MatrixType & | dF, | ||
| HessianType & | h, | ||
| ScalarType & | in_out_time | ||
| ) |
Computes value of Poincare Map, derivative and hessian of the flow.
- Parameters
-
[in] v - vector at which we want compute Poincare map [out] dF - derivative of the flow evaluated at (v,returnTime). [out] h - second order Taylor coefficients of flow evaluated at (v,returnTime). [in,out] in_out_time - on input it should specify initial time for integration for nonautonomous flows. For autonomous systems it should be initialized by zero. On output it contains approximate time at which intersection with Poincare section occurred.
◆ operator()() [41/43]
| BasicPoincareMap< SolverT, FunT >::VectorType capd::poincare::BasicPoincareMap< SolverT, FunT >::operator() | ( | VectorType | v, |
| MatrixType & | dF, | ||
| ScalarType & | in_out_time | ||
| ) |
Computes value of Poincare Map and derivative of the flow.
- Parameters
-
[in] v - vector at which we want compute Poincare map [out] dF - derivative of the flow evaluated at (v,returnTime). [in,out] in_out_time - on input it should specify initial time for integration for nonautonomous flows. For autonomous systems it should be initialized by zero. On output it contains approximate time at which intersection with Poincare section occurred.
◆ operator()() [42/43]
| BasicPoincareMap< SolverT, FunT >::VectorType capd::poincare::BasicPoincareMap< SolverT, FunT >::operator() | ( | VectorType | v, |
| ScalarType & | in_out_time | ||
| ) |
Computes value of Poincare Map.
- Parameters
-
[in] v - argument of Poincare map [in,out] in_out_time - on input it should specify initial time for integration for nonautonomous flows. For autonomous systems it should be initialized by zero. On output it contains approximate time at which intersection with Poincare section occurred.
- Returns
- P(v) - first intersection of the trajectory of v with Poincare section.
◆ operator()() [43/43]
| BasicPoincareMap< SolverT, FunT >::VectorType capd::poincare::BasicPoincareMap< SolverT, FunT >::operator() | ( | VectorType | v, |
| VectorType & | afterSection, | ||
| ScalarType & | in_out_time | ||
| ) |
Computes value of Poincare Map.
- Parameters
-
[in] v - argument of Poincare map [out] afterSection - on output it contains a point just after first intersection with Poincare section that might be used for further integration. [in,out] in_out_time - on input it should specify initial time for integration for nonautonomous flows. For autonomous systems it should be initialized by zero. On output it contains approximate time at which intersection with Poincare section occurred.
- Returns
- P(v) - first intersection of the trajectory of v with Poincare section.
◆ PoincareMap()
| capd::poincare::PoincareMap< SolverT, SectionT >::PoincareMap | ( | Solver & | solver, |
| SectionType & | section, | ||
| CrossingDirection | direction = Both, |
||
| const BoundType & | errorTolerance = 0.1 |
||
| ) |
Constructs PoincareMap for given dynamical system and section.
- Parameters
-
ds dynamical system section Poincare section crossing section crossing direction factor time step correction factor during section crossing (should be in interval (0, 1))
◆ setBlowUpMaxNorm()
|
inline |
Sets threshold value of 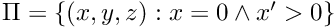 norm that is considered as a blow up of the solution. A trajectory may escape to infinity in finite time without crossing Poincare section. If the
norm that is considered as a blow up of the solution. A trajectory may escape to infinity in finite time without crossing Poincare section. If the 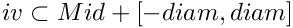 norm of a point on trajectory is bigger than this threshold value then an exception is thrown.
norm of a point on trajectory is bigger than this threshold value then an exception is thrown.
Default value is blowUpMaxNorm = 1e+10.
◆ setFactor()
|
inline |
◆ setMaxReturnTime()
|
inline |
Sets maximal return time to Poincare section. If the trajectory does not reach the section during time [0,maxReturnTime] then an exception is thrown. This prevents looping of the procedure computing Poincare map in the case when the trajectory is captured by an attractor (like sink or attracting periodic orbit) and never intersect Poincare section.
Default value is maxReturnTime = 1000.
◆ setOrder() [1/2]
|
inline |
sets new order of numerical method
◆ setOrder() [2/2]
|
inline |
Sets order of Taylor method.
◆ setSection()
|
inline |
Sets new section function.
◆ setStep() [1/2]
|
inline |
Sets step of numerical method (does make sense only when step control is disabled)
◆ setStep() [2/2]
|
inline |
Sets time step for integration of DS.
◆ stopAfterStep()
|
inline |
For dense output. If true, integration procedure returns after each successful step. The computation can be then resumed - see examples.
◆ TimeMap()
| capd::poincare::TimeMap< SolverT >::TimeMap | ( | Solver & | solver | ) |
◆ turnOffStepControl() [1/2]
|
inline |
Enables automatic step control. Step control strategy is builded into the dynamical system.
◆ turnOffStepControl() [2/2]
|
inline |
Enables automatic step control. Step control strategy is built in the solver.
◆ turnOnStepControl() [1/2]
|
inline |
Disables automatic step control.
◆ turnOnStepControl() [2/2]
|
inline |
Disables automatic step control.
◆ updateEnclosure() [1/3]
| void capd::poincare::SectionDerivativesEnclosure< MatrixT >::updateEnclosure | ( | C1Set & | prev, |
| C1Set & | next | ||
| ) |
◆ updateEnclosure() [2/3]
| void capd::poincare::SectionDerivativesEnclosure< MatrixT >::updateEnclosure | ( | C2Set & | prev, |
| C2Set & | next | ||
| ) |
◆ updateEnclosure() [3/3]
| void capd::poincare::SectionDerivativesEnclosure< MatrixT >::updateEnclosure | ( | CnSet & | prev, |
| CnSet & | next | ||
| ) |
Variable Documentation
◆ fr
| Frame fr |
◆ maxx
| double maxx = 1.6 |
◆ maxy
| double maxy = 2. |
◆ minx
| double minx = -2.2 |
◆ miny
| double miny = -2.6 |
◆ txt
| Frame txt |
