CAPD DynSys Library  5.2.0
Public Types | Public Member Functions | List of all members
capd::poincare::AbstractSection< MatrixT > Class Template Referenceabstract
Poincare

PoicareSection is class that is default PoincareSection for class PoincareMap. More...

#include <capd/poincare/AbstractSection.h>

Public Types

typedef MatrixT MatrixType
 
typedef MatrixType::RowVectorType VectorType
 
typedef MatrixType::ScalarType ScalarType
 
typedef VectorType::size_type size_type
 integral type used to index containers (vectors, matrices, etc) More...
 
typedef capd::dynset::AbstractSet< VectorType > Set
 type of abstract base class for all sets More...
 
typedef capd::diffAlgebra::Hessian< ScalarType, VectorType::csDim, VectorType::csDim > HessianType
 
typedef capd::diffAlgebra::Jet< MatrixT, 0 > JetType
 
typedef SectionDerivativesEnclosure< MatrixType > SectionDerivativesEnclosureType
 

Public Member Functions

virtual ~AbstractSection ()
 
virtual ScalarType operator() (const VectorType &v) const =0
 evaluates function at a given vector More...
 
virtual VectorType gradient (const VectorType &u) const =0
 returns gradient of the function computed at vector u More...
 
virtual ScalarType gradientByVector (const VectorType &x, const VectorType &u) const
 
virtual bool isSpecialSection () const
 This is very important function. More...
 
virtual ScalarType evalAt (const Set &set) const =0
 This function computes value of section function on a given set. More...
 
virtual void computeDT (const MatrixType &derivativeOfFlow, const VectorType &gradientOnPx, const ScalarType &denominator, VectorType &result) const
 computes gradient of return time More...
 
virtual MatrixType computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, const VectorType &fieldOnPx, VectorType &dT) const
 Simultaneous computation of gradient of return time and derivative of Poincare Map dP. More...
 
virtual void computeDP (const VectorType &Px, const MatrixType &derivativeOfFlow, const HessianType &hessianOfFlow, const VectorType &fieldOnPx, const VectorType &d2Phidt2, const MatrixType &derOfVectorFieldOnPx, MatrixType &DP, HessianType &D2P, VectorType &dT, MatrixType &d2T) const
 Simultaneous computation of first and second Taylor coefficients of return time and Poincare map. More...
 

Detailed Description

template<class MatrixT>
class capd::poincare::AbstractSection< MatrixT >

PoicareSection is class that is default PoincareSection for class PoincareMap.

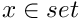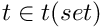Internally it wraps a functional object $ \alpha: R^n\to R $. The Poincare section is defined as $ \Pi := \alpha^{-1}(0) $.

This class provides methods for checking the sign of 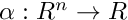$ \alpha $ evaluated at a point or a set. Efficient implementation of 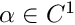$ \alpha(set) $ depends on representation of the set.

This class provides also methods for recomputation of partial derivatives of the flow to partial derivatives of Poincare map.

Let

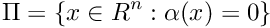  • $ \varphi(t, x): R \times R^n -> R^n $ be a dynamical system generated by given vector field.
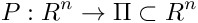  • $ s: R^n \to R $ be a section function,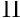
  • $ S = \{x \in R^n : s(x) = 0\} $
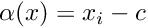  • $ P: S \to S $ be a Poincare Map
  • for given point 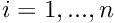$ x \in S $ let T(x) be first return time (in given crossing direction) i.e.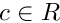 $ P(x) = \varphi(T(x), x) \in S $

In the following we denote by

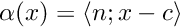
  • dP the derivative of Poincare Map P : $ dP(x) = \frac{\partial P(x)}{\partial x} $
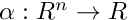
  • dT the derivative of T(x) : $ dT(x) = \frac{\partial T(x)}{\partial x} $
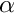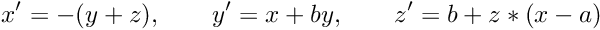
  • dF the derivative of the flow : $ dF(x) = \frac{\partial \varphi(T(x), x)}{\partial x} $ Then $ dP = dF + \frac{\partial \varphi}{\partial t} dT $

Member Typedef Documentation

◆ HessianType

template<class MatrixT >
typedef capd::diffAlgebra::Hessian<ScalarType,VectorType::csDim,VectorType::csDim> capd::poincare::AbstractSection< MatrixT >::HessianType

◆ JetType

template<class MatrixT >
typedef capd::diffAlgebra::Jet<MatrixT,0> capd::poincare::AbstractSection< MatrixT >::JetType

◆ MatrixType

template<class MatrixT >
typedef MatrixT capd::poincare::AbstractSection< MatrixT >::MatrixType

◆ ScalarType

template<class MatrixT >
typedef MatrixType::ScalarType capd::poincare::AbstractSection< MatrixT >::ScalarType

◆ SectionDerivativesEnclosureType

template<class MatrixT >
typedef SectionDerivativesEnclosure<MatrixType> capd::poincare::AbstractSection< MatrixT >::SectionDerivativesEnclosureType

◆ Set

template<class MatrixT >
typedef capd::dynset::AbstractSet<VectorType> capd::poincare::AbstractSection< MatrixT >::Set

type of abstract base class for all sets

◆ size_type

template<class MatrixT >
typedef VectorType::size_type capd::poincare::AbstractSection< MatrixT >::size_type

integral type used to index containers (vectors, matrices, etc)

◆ VectorType

template<class MatrixT >
typedef MatrixType::RowVectorType capd::poincare::AbstractSection< MatrixT >::VectorType

Constructor & Destructor Documentation

◆ ~AbstractSection()

template<class MatrixT >
virtual capd::poincare::AbstractSection< MatrixT >::~AbstractSection ( )
inlinevirtual

Member Function Documentation

◆ evalAt()

template<class MatrixT >
virtual ScalarType capd::poincare::AbstractSection< MatrixT >::evalAt ( const Set &  set) const
pure virtual

This function computes value of section function on a given set.

◆ gradient()

template<class MatrixT >
virtual VectorType capd::poincare::AbstractSection< MatrixT >::gradient ( const VectorType &  u) const
pure virtual

returns gradient of the function computed at vector u

Implemented in capd::poincare::NonlinearSection< MatrixT >, capd::poincare::CoordinateSection< MatrixT >, capd::poincare::CoordinateSection< MatrixType >, capd::poincare::AffineSection< MatrixT >, and capd::poincare::AffineSection< MatrixType >.

◆ gradientByVector()

template<class MatrixT >
virtual ScalarType capd::poincare::AbstractSection< MatrixT >::gradientByVector ( const VectorType &  x,
const VectorType &  u 
) const
inlinevirtual

Reimplemented in capd::poincare::CoordinateSection< MatrixT >, and capd::poincare::CoordinateSection< MatrixType >.

◆ isSpecialSection()

template<class MatrixT >
virtual bool capd::poincare::AbstractSection< MatrixT >::isSpecialSection ( ) const
inlinevirtual

This is very important function.

If it returns true, class PoincareMap delegates computation of value of section(set) to the section. Otherwise it is assumed that the set has more information to compute value of section(set) in most optimal way. This is quite natural as the set knows its own representation. This function returns true for instance if the PoincareSection is given by x_i=c, where x_i is i-th coordinate and c is constant.

Reimplemented in capd::poincare::CoordinateSection< MatrixT >, and capd::poincare::CoordinateSection< MatrixType >.

◆ operator()()

template<class MatrixT >
virtual ScalarType capd::poincare::AbstractSection< MatrixT >::operator() ( const VectorType &  v) const
pure virtual

evaluates function at a given vector

Implemented in capd::poincare::NonlinearSection< MatrixT >, capd::poincare::CoordinateSection< MatrixT >, capd::poincare::CoordinateSection< MatrixType >, capd::poincare::AffineSection< MatrixT >, and capd::poincare::AffineSection< MatrixType >.