This class is used to represent a map 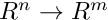$ f:R^N->R^M $ . More...

#include <capd/map/Map.h>

Public Types
typedef MatrixT	MatrixType
	public type: Matrix used in the computations (template parameter) More...

typedef MatrixType::RowVectorType	VectorType
	public type: Vector that represent arguments of the map (dimension is equal to number of variables) More...

typedef MatrixType::ColumnVectorType	ImageVectorType
	public type: Vector that represent value of the map (dimension is equal to number of functions) More...

typedef MatrixType::RefColumnVectorType	RefColumnVectorType
	public type: reference vector that represent value of the map (dimension is equal to number of functions) More...

typedef VectorType::ScalarType	ScalarType

typedef Function< VectorType >	FunctionType

typedef capd::autodiff::DagIndexer< ScalarType >	DAG

typedef capd::autodiff::Node	NodeType

typedef BasicFunction< ScalarType >	BaseFunction

typedef capd::diffAlgebra::Hessian< ScalarType, ImageVectorType::csDim, VectorType::csDim >	HessianType

typedef capd::diffAlgebra::Jet< MatrixT, 0 >	JetType

typedef BaseFunction::size_type	size_type

Public Member Functions
	Map ()
	creates an univariate function R->R, f(x)=0 More...

	Map (const std::string &, size_type degree=1)
	parses expression from given string. Allocates memory for jet propagation of degree 'degree' More...

	Map (const char *, size_type degree=1)
	parses expression from given string. Allocates memory for jet propagation of degree 'degree' More...

	Map (const Map &f)
	copying constructor More...

template<typename Function >
	Map (Function f, int dimIn, int dimOut, int noParam, size_type degree=1)
	parses expression from given routine. More...

Map &	operator= (const char *)
	parses expression from a given string and reallocates DAG, does not change already specified degree More...

Map &	operator= (const std::string &)
	parses expression from a given string and reallocates DAG, does not change already specified degree More...

Map &	operator= (const Map &f)
	assignment from an object More...

template<typename Function >
void	reset (Function f, int dimIn, int dimOut, int noParam, size_type degree)
	parses expression from given routine. More...

template<typename Function >
void	reset (Function f, int dimIn, int dimOut, int noParam)
	parses expression from given routine. More...

ImageVectorType	operator() (const VectorType &u) const
	evaluates map at a given vector. More...

ImageVectorType	operator() (ScalarType t, const VectorType &u) const
	evaluates at a given vector and for given time More...

ImageVectorType	operator() (const VectorType &u, MatrixType &out_derivative) const
	computes simultaneously value and derivative of the map for a given vector More...

ImageVectorType	operator() (ScalarType t, const VectorType &u, MatrixType &out_derivative) const
	computes simultaneously value and derivative of the map for a given vector and time More...

MatrixType	operator[] (const VectorType &u) const
	computes derivative of the map for a given vector More...

MatrixType	derivative (const VectorType &u) const
	computes derivative of the map for a given vector More...

MatrixType	derivative (ScalarType t, const VectorType &u) const
	computes derivative of the map for a given vector and time More...

void	homogenousPolynomial (MatrixType &o_der) const
	Computes derivative of the map at a vector 'u' that was send to any vector or function evaluating value. More...

void	homogenousPolynomial (const MatrixType &o_der, HessianType &o_hessian) const
	Computes derivative and hessian of the map at a vector 'u' that was send to any vector or function evaluating value. More...

template<class JetT >
void	homogenousPolynomial (JetT &x, size_type degree) const
	Computes jet to degree 'degree' of the map at a vector 'u', at which the map was previously evaluated. More...

ImageVectorType	operator() (const VectorType &x, MatrixType &out_df, HessianType &out_hf) const
	computes value, first and second order derivatives for a given vector More...

ImageVectorType	operator() (ScalarType t, const VectorType &x, MatrixType &out_df, HessianType &out_hf) const
	computes value, first and second order derivatives for a given vector and time More...

JetType	operator() (const JetType &x) const
	computes propagation of the jet x through the map and returns jet of normalized partial derivatives of the function 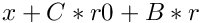$f\circ x$ . More...

JetType	operator() (ScalarType t, const JetType &x) const
	computes propagation of the jet x through the map and returns jet of normalized partial derivatives of the function 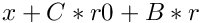$f\circ x$ . More...

ImageVectorType	operator() (const VectorType &x, JetType &out_jet) const

ImageVectorType	operator() (ScalarType t, const VectorType &x, JetType &out_jet) const

void	computeODECoefficients (VectorType coeffs[], size_type order) const
	iterative computation of Taylor coefficients up to given order for a solution to ODE represented by this map. More...

void	computeODECoefficients (VectorType coeffs[], MatrixType dCoeffs[], size_type order) const
	iterative computation of Taylor coefficients up to given order for a solution to ODE represented by this map together with first order variational equations More...

void	computeODECoefficients (VectorType coeffs[], MatrixType dCoeffs[], HessianType hCoeffs[], size_type order) const
	iterative computation of Taylor coefficients up to given order for a solution to ODE represented by this map together with first and second order variational equations More...

void	computeODECoefficients (JetType coeffs[], size_type degree, size_type order) const
	Iterative computation of Taylor coefficients up to given order for a solution to ODE and its variational equations. More...

void	setParameters (const VectorType &values)
	simultaneously sets values of many parameters. It is assumed that given vector contains values of subsequent parameters. More...

void	setDegree (size_type degree)
	set maximal order of space-derivatives that the map can compute. More...

void	codeTranslation (const char className[], const char userNamespace[], const char relativePath[]=".", size_type maxTimeOrder=32) const
	This method generates code of new class in which DAG is constructed as static array, dimensions are fixed giving the compiler chance for most aggressive optimization. More...

void	setOrder (size_type)
	allocates necessary memory for ODE solver of order 'order' More...

void	setParameter (size_type d, const MatrixT::ScalarType &value)
	sets new value of a parameter of index d. More...

void	setParameter (const std::string &name, const ScalarType &value)
	sets new value of a parameter. If parameter not found there is no effect. More...

void	setParameters (const MatrixT::ScalarType *values, size_type d)
	simultaneously sets values of many parameters. It is assumed that given vector contains values of subsequent parameters. More...

ScalarType	getParameter (size_type d) const

ScalarType	getParameter (const std::string &name) const

void	setCurrentTime (const ScalarType &a_time) const
	sets actual value of variable that represents time in an ODE. More...

const ScalarType &	getCurrentTime () const
	returns actual value of variable that represents time in an ODE More...

void	differentiateTime () const
	sets first derivative of time with respect to time equal to 1 More...

void	setMask (Iterator b, Iterator e)
	The iterator range [b,e) should contain a range of Multiinideces the user requires to compute. More...

void	addMultiindexToMask (const capd::vectalg::Multiindex &mi)
	Adds new multiindex (along with dependencies) to the existing mask. More...

void	resetMask ()
	Resets the mask of derivatives. More...

const bool *	getMask () const

bool	getMask (size_type i) const

bool	getMask (size_type i, size_type j) const

Protected Member Functions
void	generateHeaderFile (const char className[], const char userNamespace[], const char relativePath[], size_type maxTimeOrder=32) const

void	generateHppFile (const char className[], const char userNamespace[], const char relativePath[], size_type maxTimeOrder=32) const

void	generateCppFile (const char className[], const char userNamespace[], const char relativePath[], size_type maxTimeOrder=32) const

void	evalAndCopyResult (JetType &c) const

void	checkDegree (size_type degree) const

void	checkOrder (size_type order) const

void	createDefault ()
	used to create a default object without expression. Creates a univariate constant function f(x)=0 More...

void	createFromText (std::string s)
	parses expression from given string. Allocates memory for ODE solver of order 'order' More...

void	copyObject (const BasicFunction &f)
	an auxiliary function used in copying constructor and assignment operator More...

void	clean ()
	resets all allocated data More...

void	realloc (size_type degree)
	reallocates memory for computation of derivatives up to order 'degree' More...

void	setArgument (const V &v) const

void	applyC1Mask () const

void	evalHomogenousPolynomial () const

void	evalHomogenousPolynomial (size_type degree, size_type coeffNo=0) const

void	eval (size_type coeffNo) const

void	eval (size_type degree, size_type coeffNo) const

void	deleteNodes ()

Protected Attributes
size_type	m_degree
	maximal order of derivatives that the map can compute More...

std::vector< capd::autodiff::AbstractNode< ScalarType > * >	m_nodes

std::vector< capd::autodiff::Node >	m_fullGraph
	graph representing the expression More...

std::vector< capd::autodiff::MyNode >	m_evalPath
	reduced graph - only nodes with nontrivial evaluations are left More...

std::vector< int >	m_pos
	indices of roots of expressions for each component More...

std::vector< std::string >	m_var
	variables, time and parameters More...

DAG	m_dag
	data structure that stores all the coefficients. Provides suitable indexing and evaluation of expression. More...

size_type	m_indexOfFirstParam
	if equal to m_var.size() then no parameters specified More...

Detailed Description

template<typename MatrixT>
class capd::map::Map< MatrixT >

This class is used to represent a map 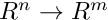$ f:R^N->R^M $ .

The class provides methods for:

computation of Taylor coefficients of the map at a given vector up to given degree
computing first order derivative and hessian
jet propagation through the map

The map is parsed from a human readable string. Syntax of the formula:

"[par:a,b,c...;][time:t;]var:x1,x2,...;fun:expression1,expression2,....;"

Sections par and time are optional.

var - names of subsequent arguments
fun - expressions that define a map. You can use most elementary functions: sin, cos, exp, log, sqrt, sqr operators: +,-,*,/,^ (power, integer or not. Exponent cannot depend on variables - we assume gradient of exponent is zero). constants: (0,1,2,-5,2.5,-0.25, etc)- we recommend usage of representable numbers only. If a constant is an interval or a floating point represented with high precision, one should use a parameter instead.
par - parameters of the map. Derivatives of them with respect to main variables are assumed to be zero.
time - a distinguished parameter with derivative dt/dt=1. Used for nonautonomous ODEs

Dimensions N and M are automatically recognized from the number of variables and functions.

Note: If MatrixT is of fixed dimensions (R,C) then these numbers MUST agree (R,C)=(M,N).

Example:

#include "capd/capdlib.h"
std::string lorenzFormula("par:s,r,q;var:x,y,z;fun:s*(y-x),x*(r-z)-y,x*y-q*z;");
capd::IMap lorenz(lorenzFormula);
lorenz.setParameter("s",10.);
lorenz.setParameter("r",28.);
lorenz.setParameter("q",interval(8.)/interval(3.));

The map can be parsed from a C-like routine. One has to write a global function that defines map and pass it to the constructor. The function that defines a map must have the following signature:

#include "capd/capdlib.h"
void vf(capd::autodiff::Node t,
        capd::autodiff::Node in[], int dimIn,
        capd::autodiff::Node out[], int dimOut,
        capd::autodiff::Node params[], int noParam
       );

Here:

t - is a time, required for non-autonomous ODEs
in - is a C-array of input variables
dimIn - is number of input variables
out - is a C-array of output variables
dimOut - is number of output variables
params - is a C-array of parameters
noParam - is number of parameters

Example:

#include "capd/capdlib.h"
using capd::autodiff::Node;
void lorenzVectorField(Node t, Node in[], int dimIn, Node out[], int dimOut, Node params[], int noParams)
{
  out[0] = params[0]*(in[1]-in[0]);
  out[1] = in[0]*(params[1]-in[2])-in[1];
  out[2] = in[1]*in[2]-params[2]*in[2];
}
 
int dimIn=3, dimOut=3, noParam=3;
capd::IMap lorenz(lorenzVectorField,dimIn,dimOut,noParam);
lorenz.setParameter(0,10.);
lorenz.setParameter(1,28.);
lorenz.setParameter(2,interval(8.)/interval(3.));

This class can be used as a vector field defining an ODE. It provides methods for computation of Taylor coefficients of solutions to ODEs and associated variational equations. Although the user can define own ODE solver based on computed coefficients by class Map, we recommend to use class capd::dynsys::BasicTaylor and inherited from it. These classes provide suitable interface for integration of ODEs and variational equations.

About implementation.

Directed acyclic graph (DAG) that encodes a map is stored as well indexed array. Thus processing of it is fast. Moreover, this representation is well suited for:

GPU computing (simple array allocation on the device)
source translation techniques During parsing process the expressions are optimized. Thus subexpressions that appear many times in these formulas are computed only once. For example in the vector field:
std::string twistedOScillator("var:x,y;fun:y*(x^2+y^2),-x*(x^2+y^2);");

subexpression x^2+y^2 is recognized and computed only once.

Remarks: The parser does not perform factorization of expressions.

Member Typedef Documentation

◆ BaseFunction

template<typename MatrixT >

typedef BasicFunction<ScalarType> capd::map::Map< MatrixT >::BaseFunction

◆ DAG

template<typename MatrixT >

typedef capd::autodiff::DagIndexer<ScalarType> capd::map::Map< MatrixT >::DAG

◆ FunctionType

template<typename MatrixT >

typedef Function<VectorType> capd::map::Map< MatrixT >::FunctionType

◆ HessianType

template<typename MatrixT >

typedef capd::diffAlgebra::Hessian<ScalarType,ImageVectorType::csDim,VectorType::csDim> capd::map::Map< MatrixT >::HessianType

◆ ImageVectorType

template<typename MatrixT >

typedef MatrixType::ColumnVectorType capd::map::Map< MatrixT >::ImageVectorType

public type: Vector that represent value of the map (dimension is equal to number of functions)

◆ JetType

template<typename MatrixT >

typedef capd::diffAlgebra::Jet<MatrixT,0> capd::map::Map< MatrixT >::JetType

◆ MatrixType

template<typename MatrixT >

typedef MatrixT capd::map::Map< MatrixT >::MatrixType

public type: Matrix used in the computations (template parameter)

◆ NodeType

template<typename MatrixT >

typedef capd::autodiff::Node capd::map::Map< MatrixT >::NodeType

◆ RefColumnVectorType

template<typename MatrixT >

typedef MatrixType::RefColumnVectorType capd::map::Map< MatrixT >::RefColumnVectorType

public type: reference vector that represent value of the map (dimension is equal to number of functions)

◆ ScalarType

template<typename MatrixT >

typedef VectorType::ScalarType capd::map::Map< MatrixT >::ScalarType

◆ size_type

template<typename MatrixT >

typedef BaseFunction::size_type capd::map::Map< MatrixT >::size_type

◆ VectorType

template<typename MatrixT >

typedef MatrixType::RowVectorType capd::map::Map< MatrixT >::VectorType

public type: Vector that represent arguments of the map (dimension is equal to number of variables)

Constructor & Destructor Documentation

◆ Map() [1/5]

template<typename MatrixT >

capd::map::Map< MatrixT >::Map

creates an univariate function R->R, f(x)=0

◆ Map() [2/5]

template<typename MatrixT >

capd::map::Map< MatrixT >::Map	(	const std::string &	f,
		size_type	degree = `1`
	)

parses expression from given string. Allocates memory for jet propagation of degree 'degree'

◆ Map() [3/5]

template<typename MatrixT >

capd::map::Map< MatrixT >::Map	(	const char *	s,
		size_type	degree = `1`
	)

parses expression from given string. Allocates memory for jet propagation of degree 'degree'

◆ Map() [4/5]

template<typename MatrixT >

capd::map::Map< MatrixT >::Map ( const Map< MatrixT > & f )

copying constructor

◆ Map() [5/5]

template<typename MatrixT >

template<typename Function >

capd::map::Map< MatrixT >::Map	(	Function	f,
		int	dimIn,
		int	dimOut,
		int	noParam,
		size_type	degree = `1`
	)

inline

parses expression from given routine.

Allocates memory for jet propagation of degree 'degree'

Parameters

f	routine that defines function, its signature is: void (NodeType time, NodeType in[], int dimIn, NodeType out[], int dimOut, NodeType param[], int noParam)
dimIn	number of input variables (dimension of domain)
dimOut	number of output variables (dimension of codomain)
noParam	number of parameters
degree	maximal degree of derivatives that can be computed

Member Function Documentation

◆ addMultiindexToMask()

void capd::map::BasicFunction< MatrixT::ScalarType >::addMultiindexToMask ( const capd::vectalg::Multiindex & mi )

inlineinherited

Adds new multiindex (along with dependencies) to the existing mask.

Parameters

mi	multiindex to be added to the mask

Warning: causes undefined behavior if the mask has not been set before call to this method.

◆ applyC1Mask()

void capd::map::BasicFunction< MatrixT::ScalarType >::applyC1Mask

protectedinherited

◆ checkDegree()

template<typename MatrixT >

void capd::map::Map< MatrixT >::checkDegree ( size_type degree ) const

inlineprotected

◆ checkOrder()

template<typename MatrixT >

void capd::map::Map< MatrixT >::checkOrder ( size_type order ) const

inlineprotected

◆ clean()

void capd::map::BasicFunction< MatrixT::ScalarType >::clean

protectedinherited

resets all allocated data

◆ codeTranslation()

template<typename MatrixT >

void capd::map::Map< MatrixT >::codeTranslation	(	const char	className[],
		const char	userNamespace[],
		const char	relativePath[] = `"."`,
		size_type	maxTimeOrder = `32`
	)		const

This method generates code of new class in which DAG is constructed as static array, dimensions are fixed giving the compiler chance for most aggressive optimization.

This method is used to speed up your computation. DAG that represents an expression is allocated dynamically and thus its processing might be not that fast as in hand optimized code.

Parameters

[in]	className	- name of the class that will be generated. The code will be generated into file realativePath/className.h.
[in]	relativePath	- path to folder where generated code will be save
[in]	userNamespace	- must be specified - the code will be put into this namespace.

Attention: The method does not check whether arguments are correct identifiers in C++.

◆ computeODECoefficients() [1/4]

template<typename MatrixT >

void capd::map::Map< MatrixT >::computeODECoefficients	(	JetType	coeffs[],
		size_type	degree,
		size_type	order
	)		const

Iterative computation of Taylor coefficients up to given order for a solution to ODE and its variational equations.

Parameters

	degree	- The maximal order of derivatives with respect to initial conditions is specified by this argument
	order	- order of Taylor method (degree of polynomial approximation to the solution)
[in,out]	coeffs[0]	- jets of initial conditions for the solution and all variational equations, coeffs[1],...,coeffs[order] - computed coefficients of polynomial approximation to the solution all variational equations

Note: coeffs[i] can be a jet of degree bigger than the argument 'degree'.

◆ computeODECoefficients() [2/4]

template<typename MatrixT >

void capd::map::Map< MatrixT >::computeODECoefficients	(	VectorType	coeffs[],
		MatrixType	dCoeffs[],
		HessianType	hCoeffs[],
		size_type	order
	)		const

iterative computation of Taylor coefficients up to given order for a solution to ODE represented by this map together with first and second order variational equations

Parameters

	order	- order of Taylor method (degree of polynomial approximation to the solution)
[in]	coeffs[0]	- initial condition for ODE must be the first vector in the table
[out]	coeffs[1],...,coeffs[order]	- computed coefficients of polynomial approximation
[in]	dCoeffs[0]	- initial condition for variational equation
[out]	dCoeffs[1],...,dCoeffs[order]	- computed coefficients of polynomial approximation to the solution to variational equation
[in]	hCoeffs[0]	- initial condition for second order variational equation
[out]	hCoeffs[1],...,hCoeffs[order]	- computed coefficients of polynomial approximation to the solution to second order variational equation

Note: Second order variational equations are written in the base of normalized derivatives (Taylor coefficients). To obtain derivatives of solution wrt to initial condition one must multiply them by suitable factorials. iterative computation of Taylor coefficients up to given order for a solution to ODE, first and second order variational equations

◆ computeODECoefficients() [3/4]

template<typename MatrixT >

void capd::map::Map< MatrixT >::computeODECoefficients	(	VectorType	coeffs[],
		MatrixType	dCoeffs[],
		size_type	order
	)		const

iterative computation of Taylor coefficients up to given order for a solution to ODE represented by this map together with first order variational equations

Parameters

	order	- order of Taylor method (degree of polynomial approximation to the solution)
[in]	coeffs[0]	- initial condition for ODE must be the first vector in the table
[out]	coeffs[1],...,coeffs[order]	- computed coefficients of polynomial approximation
[in]	dCoeffs[0]	- initial condition for variational equation
[out]	dCoeffs[1],...,dCoeffs[order]	- computed coefficients of polynomial approximation to the solution to variational equation

◆ computeODECoefficients() [4/4]

template<typename MatrixT >

void capd::map::Map< MatrixT >::computeODECoefficients	(	VectorType	coeffs[],
		size_type	order
	)		const

iterative computation of Taylor coefficients up to given order for a solution to ODE represented by this map.

Parameters

	order	- order of Taylor method (degree of polynomial approximation to the solution)
[in]	coeffs[0]	- initial condition for ODE must be the first vector in the table
[out]	coeffs[1],...,coeffs[order]	- computed coefficients of polynomial approximation

◆ copyObject()

void capd::map::BasicFunction< MatrixT::ScalarType >::copyObject ( const BasicFunction< MatrixT::ScalarType > & f )

protectedinherited

an auxiliary function used in copying constructor and assignment operator

◆ createDefault()

void capd::map::BasicFunction< MatrixT::ScalarType >::createDefault

protectedinherited

used to create a default object without expression. Creates a univariate constant function f(x)=0

◆ createFromText()

void capd::map::BasicFunction< MatrixT::ScalarType >::createFromText ( std::string s )

protectedinherited

parses expression from given string. Allocates memory for ODE solver of order 'order'

◆ deleteNodes()

void capd::map::BasicFunction< MatrixT::ScalarType >::deleteNodes

protectedinherited

◆ derivative() [1/2]

template<typename MatrixT >

MatrixT capd::map::Map< MatrixT >::derivative ( const VectorType & u ) const

inline

computes derivative of the map for a given vector

◆ derivative() [2/2]

template<typename MatrixT >

MatrixT capd::map::Map< MatrixT >::derivative	(	ScalarType	t,
		const VectorType &	u
	)		const

inline

computes derivative of the map for a given vector and time

◆ differentiateTime()

void capd::map::BasicFunction< MatrixT::ScalarType >::differentiateTime

inherited

sets first derivative of time with respect to time equal to 1

◆ eval() [1/2]

void capd::map::BasicFunction< MatrixT::ScalarType >::eval ( size_type coeffNo ) const

inlineprotectedinherited

◆ eval() [2/2]

void capd::map::BasicFunction< MatrixT::ScalarType >::eval	(	size_type	degree,
		size_type	coeffNo
	)		const

inlineprotectedinherited

◆ evalAndCopyResult()

template<typename MatrixT >

void capd::map::Map< MatrixT >::evalAndCopyResult ( JetType & c ) const

protected

◆ evalHomogenousPolynomial() [1/2]

void capd::map::BasicFunction< MatrixT::ScalarType >::evalHomogenousPolynomial

inlineprotectedinherited

◆ evalHomogenousPolynomial() [2/2]

void capd::map::BasicFunction< MatrixT::ScalarType >::evalHomogenousPolynomial	(	size_type	degree,
		size_type	coeffNo = `0`
	)		const

inlineprotectedinherited

◆ generateCppFile()

template<typename MatrixT >

void capd::map::Map< MatrixT >::generateCppFile	(	const char	className[],
		const char	userNamespace[],
		const char	relativePath[],
		size_type	maxTimeOrder = `32`
	)		const

protected

◆ generateHeaderFile()

template<typename MatrixT >

void capd::map::Map< MatrixT >::generateHeaderFile	(	const char	className[],
		const char	userNamespace[],
		const char	relativePath[],
		size_type	maxTimeOrder = `32`
	)		const

protected

◆ generateHppFile()

template<typename MatrixT >

void capd::map::Map< MatrixT >::generateHppFile	(	const char	className[],
		const char	userNamespace[],
		const char	relativePath[],
		size_type	maxTimeOrder = `32`
	)		const

protected

◆ getCurrentTime()

const MatrixT::ScalarType & capd::map::BasicFunction< MatrixT::ScalarType >::getCurrentTime

inherited

returns actual value of variable that represents time in an ODE

◆ getMask() [1/3]

const bool* capd::map::BasicFunction< MatrixT::ScalarType >::getMask

inlineinherited

◆ getMask() [2/3]

bool capd::map::BasicFunction< MatrixT::ScalarType >::getMask ( size_type i ) const

inlineinherited

◆ getMask() [3/3]

bool capd::map::BasicFunction< MatrixT::ScalarType >::getMask	(	size_type	i,
		size_type	j
	)		const

inlineinherited

◆ getParameter() [1/2]

BasicFunction< MatrixT::ScalarType >::ScalarType capd::map::BasicFunction< MatrixT::ScalarType >::getParameter ( const std::string & name ) const

inherited

◆ getParameter() [2/2]

BasicFunction< MatrixT::ScalarType >::ScalarType capd::map::BasicFunction< MatrixT::ScalarType >::getParameter ( size_type d ) const

inherited

◆ homogenousPolynomial() [1/3]

template<typename MatrixT >

void capd::map::Map< MatrixT >::homogenousPolynomial	(	const MatrixType &	o_der,
		HessianType &	o_hessian
	)		const

Computes derivative and hessian of the map at a vector 'u' that was send to any vector or function evaluating value.

In this case computation can be speeded up.

◆ homogenousPolynomial() [2/3]

template<typename MatrixT >

template<class JetT >

void capd::map::Map< MatrixT >::homogenousPolynomial	(	JetT &	x,
		size_type	degree
	)		const

Computes jet to degree 'degree' of the map at a vector 'u', at which the map was previously evaluated.

In this case computation can be speeded up.

◆ homogenousPolynomial() [3/3]

template<typename MatrixT >

void capd::map::Map< MatrixT >::homogenousPolynomial ( MatrixType & o_der ) const

Computes derivative of the map at a vector 'u' that was send to any vector or function evaluating value.

In this case computation can be speeded up.

◆ operator()() [1/10]

template<typename MatrixT >

Map< MatrixT >::JetType capd::map::Map< MatrixT >::operator() ( const JetType & x ) const

computes propagation of the jet x through the map and returns jet of normalized partial derivatives of the function 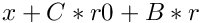$f\circ x$ .

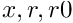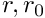Note: if with $N\neq M$ then input and output jets have different dimensions.

◆ operator()() [2/10]

template<typename MatrixT >

Map< MatrixT >::ImageVectorType capd::map::Map< MatrixT >::operator() ( const VectorType & u ) const

evaluates map at a given vector.

◆ operator()() [3/10]

template<typename MatrixT >

Map< MatrixT >::ImageVectorType capd::map::Map< MatrixT >::operator()	(	const VectorType &	u,
		MatrixType &	out_derivative
	)		const

computes simultaneously value and derivative of the map for a given vector

◆ operator()() [4/10]

template<typename MatrixT >

Map< MatrixT >::ImageVectorType capd::map::Map< MatrixT >::operator()	(	const VectorType &	x,
		JetType &	out_jet
	)		const

◆ operator()() [5/10]

template<typename MatrixT >

Map< MatrixT >::ImageVectorType capd::map::Map< MatrixT >::operator()	(	const VectorType &	x,
		MatrixType &	out_df,
		HessianType &	out_hf
	)		const

computes value, first and second order derivatives for a given vector

◆ operator()() [6/10]

template<typename MatrixT >

Map< MatrixT >::JetType capd::map::Map< MatrixT >::operator()	(	ScalarType	t,
		const JetType &	x
	)		const

inline

computes propagation of the jet x through the map and returns jet of normalized partial derivatives of the function 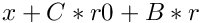$f\circ x$ .

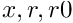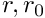Note: if with $N\neq M$ then input and output jets have different dimensions.

◆ operator()() [7/10]

template<typename MatrixT >

Map< MatrixT >::ImageVectorType capd::map::Map< MatrixT >::operator()	(	ScalarType	t,
		const VectorType &	u
	)		const

inline

evaluates at a given vector and for given time

◆ operator()() [8/10]

template<typename MatrixT >

Map< MatrixT >::ImageVectorType capd::map::Map< MatrixT >::operator()	(	ScalarType	t,
		const VectorType &	u,
		MatrixType &	out_derivative
	)		const

inline

computes simultaneously value and derivative of the map for a given vector and time

◆ operator()() [9/10]

template<typename MatrixT >

Map< MatrixT >::ImageVectorType capd::map::Map< MatrixT >::operator()	(	ScalarType	t,
		const VectorType &	x,
		JetType &	out_jet
	)		const

inline

◆ operator()() [10/10]

template<typename MatrixT >

Map< MatrixT >::ImageVectorType capd::map::Map< MatrixT >::operator()	(	ScalarType	t,
		const VectorType &	x,
		MatrixType &	out_df,
		HessianType &	out_hf
	)		const

inline

computes value, first and second order derivatives for a given vector and time

◆ operator=() [1/3]

template<typename MatrixT >

Map< MatrixT > & capd::map::Map< MatrixT >::operator= ( const char * s )

parses expression from a given string and reallocates DAG, does not change already specified degree

◆ operator=() [2/3]

template<typename MatrixT >

Map< MatrixT > & capd::map::Map< MatrixT >::operator= ( const Map< MatrixT > & f )

assignment from an object

◆ operator=() [3/3]

template<typename MatrixT >

Map< MatrixT > & capd::map::Map< MatrixT >::operator= ( const std::string & s )

parses expression from a given string and reallocates DAG, does not change already specified degree

◆ operator[]()

template<typename MatrixT >

MatrixT capd::map::Map< MatrixT >::operator[] ( const VectorType & u ) const

inline

computes derivative of the map for a given vector

◆ realloc()

void capd::map::BasicFunction< MatrixT::ScalarType >::realloc ( size_type degree )

protectedinherited

reallocates memory for computation of derivatives up to order 'degree'

◆ reset() [1/2]

template<typename MatrixT >

template<typename Function >

void capd::map::Map< MatrixT >::reset	(	Function	f,
		int	dimIn,
		int	dimOut,
		int	noParam
	)

inline

parses expression from given routine.

It does not change actual maximal degree of jets that moght be propagated by this map.

Parameters

f	- routine that defines function, its signature is: void (NodeType time, NodeType in[], int dimIn, NodeType out[], int dimOut, NodeType param[], int noParam)
dimIn	- number of input variables (dimension of domain)
dimOut	- number of output variables (dimension of codomain)
noParam	- number of parameters

◆ reset() [2/2]

template<typename MatrixT >

template<typename Function >

void capd::map::Map< MatrixT >::reset	(	Function	f,
		int	dimIn,
		int	dimOut,
		int	noParam,
		size_type	degree
	)

inline

parses expression from given routine.

Allocates memory for jet propagation of degree 'degree'

Parameters

f	- routine that defines function, its signature is: void (NodeType time, NodeType in[], int dimIn, NodeType out[], int dimOut, NodeType param[], int noParam)
dimIn	- number of input variables (dimension of domain)
dimOut	- number of output variables (dimension of codomain)
noParam	- number of parameters

◆ resetMask()

void capd::map::BasicFunction< MatrixT::ScalarType >::resetMask

inlineinherited

Resets the mask of derivatives.

In consequence, full jet of derivatives will be computed after call to any method that computes derivative, hessian or jet.

◆ setArgument()

void capd::map::BasicFunction< MatrixT::ScalarType >::setArgument ( const V & v ) const

protectedinherited

◆ setCurrentTime()

void capd::map::BasicFunction< MatrixT::ScalarType >::setCurrentTime ( const ScalarType & a_time ) const

inherited

sets actual value of variable that represents time in an ODE.

◆ setDegree()

template<typename MatrixT >

void capd::map::Map< MatrixT >::setDegree ( size_type degree )

set maximal order of space-derivatives that the map can compute.

◆ setMask()

void capd::map::BasicFunction< MatrixT::ScalarType >::setMask	(	Iterator	b,
		Iterator	e
	)

inlineinherited

The iterator range [b,e) should contain a range of Multiinideces the user requires to compute.

The method automatically adds all the depending partial derivatives to this collection and defines a mask for computation of partial derivtives.

Parameters

[b,e) iterator range which contains collection of multiindices

Warning: The method causes undefined behavior if a multiindex in the collection exceeds limits of the map (like dimension, maximal allowed degree).

◆ setOrder()

void capd::map::BasicFunction< MatrixT::ScalarType >::setOrder ( size_type order )

inherited

allocates necessary memory for ODE solver of order 'order'

◆ setParameter() [1/2]

void capd::map::BasicFunction< MatrixT::ScalarType >::setParameter	(	const std::string &	name,
		const ScalarType &	value
	)

inherited

sets new value of a parameter. If parameter not found there is no effect.

◆ setParameter() [2/2]

void capd::map::BasicFunction< MatrixT::ScalarType >::setParameter	(	size_type	d,
		const MatrixT::ScalarType &	value
	)

inherited

sets new value of a parameter of index d.

◆ setParameters() [1/2]

void capd::map::BasicFunction< MatrixT::ScalarType >::setParameters	(	const MatrixT::ScalarType *	values,
		size_type	d
	)

inherited

simultaneously sets values of many parameters. It is assumed that given vector contains values of subsequent parameters.

◆ setParameters() [2/2]

template<typename MatrixT >

void capd::map::Map< MatrixT >::setParameters ( const VectorType & values )

simultaneously sets values of many parameters. It is assumed that given vector contains values of subsequent parameters.

Member Data Documentation

◆ m_dag

DAG capd::map::BasicFunction< MatrixT::ScalarType >::m_dag

mutableprotectedinherited

data structure that stores all the coefficients. Provides suitable indexing and evaluation of expression.

◆ m_degree

template<typename MatrixT >

size_type capd::map::Map< MatrixT >::m_degree

protected

maximal order of derivatives that the map can compute

◆ m_evalPath

std::vector<capd::autodiff::MyNode> capd::map::BasicFunction< MatrixT::ScalarType >::m_evalPath

protectedinherited

reduced graph - only nodes with nontrivial evaluations are left

◆ m_fullGraph

std::vector<capd::autodiff::Node> capd::map::BasicFunction< MatrixT::ScalarType >::m_fullGraph

protectedinherited

graph representing the expression

◆ m_indexOfFirstParam

size_type capd::map::BasicFunction< MatrixT::ScalarType >::m_indexOfFirstParam

protectedinherited

if equal to m_var.size() then no parameters specified

◆ m_nodes

std::vector<capd::autodiff::AbstractNode<ScalarType>*> capd::map::BasicFunction< MatrixT::ScalarType >::m_nodes

protectedinherited

◆ m_pos

std::vector<int> capd::map::BasicFunction< MatrixT::ScalarType >::m_pos

protectedinherited

indices of roots of expressions for each component

◆ m_var

std::vector<std::string> capd::map::BasicFunction< MatrixT::ScalarType >::m_var

protectedinherited

variables, time and parameters

Public Types

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

template<typename MatrixT> class capd::map::Map< MatrixT >

Member Typedef Documentation

◆ BaseFunction

◆ DAG

◆ FunctionType

◆ HessianType

◆ ImageVectorType

◆ JetType

◆ MatrixType

◆ NodeType

◆ RefColumnVectorType

◆ ScalarType

◆ size_type

◆ VectorType

Constructor & Destructor Documentation

◆ Map() [1/5]

◆ Map() [2/5]

◆ Map() [3/5]

◆ Map() [4/5]

◆ Map() [5/5]

Member Function Documentation

◆ addMultiindexToMask()

◆ applyC1Mask()

◆ checkDegree()

◆ checkOrder()

◆ clean()

◆ codeTranslation()

◆ computeODECoefficients() [1/4]

◆ computeODECoefficients() [2/4]

◆ computeODECoefficients() [3/4]

◆ computeODECoefficients() [4/4]

◆ copyObject()

◆ createDefault()

◆ createFromText()

◆ deleteNodes()

◆ derivative() [1/2]

◆ derivative() [2/2]

◆ differentiateTime()

◆ eval() [1/2]

◆ eval() [2/2]

◆ evalAndCopyResult()

◆ evalHomogenousPolynomial() [1/2]

◆ evalHomogenousPolynomial() [2/2]

◆ generateCppFile()

◆ generateHeaderFile()

◆ generateHppFile()

◆ getCurrentTime()

◆ getMask() [1/3]

◆ getMask() [2/3]

◆ getMask() [3/3]

◆ getParameter() [1/2]

◆ getParameter() [2/2]

◆ homogenousPolynomial() [1/3]

◆ homogenousPolynomial() [2/3]

◆ homogenousPolynomial() [3/3]

◆ operator()() [1/10]

◆ operator()() [2/10]

◆ operator()() [3/10]

◆ operator()() [4/10]

◆ operator()() [5/10]

◆ operator()() [6/10]

◆ operator()() [7/10]

◆ operator()() [8/10]

◆ operator()() [9/10]

◆ operator()() [10/10]

◆ operator=() [1/3]

◆ operator=() [2/3]

◆ operator=() [3/3]

◆ operator[]()

◆ realloc()

◆ reset() [1/2]

◆ reset() [2/2]

◆ resetMask()

◆ setArgument()

◆ setCurrentTime()

template<typename MatrixT>
class capd::map::Map< MatrixT >