This example is a complete proof of the existence of 3 different periodic solution for the Rossler system

$x' = -(y+z), \qquad y' = x + by,\qquad z' = b + z*(x-a)$

with chaotic parameter values a=5.7, b=0.2.

Let us fix Poincare section 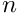$\Pi = \{(x,y,z) : x=0 \wedge x'>0\}$ and let 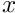$ P $ be the associated Poincare map - see picture below.

Using the Interval Newton Operator

$N(f,x_0,X) = x_0 - [Df(x)]_I^{-1} f(x_0)$

applied to the map 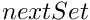$ f = P^n - Id$ we validate that 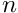$ f $ has zero for n=1,2,3. Although we do not check this in the program, these orbits are significantly different and of principal period n=1,2,3, respectively.

The source of this example can be found in the examples/RosslerPeriodicOrbit directory of the CAPD package.

Attention: This program requires C++11 compiler support, for instance gcc-4.8 or newer with -std=c++11 flag.

#include <iostream>
#include "capd/capdlib.h"
 
using namespace capd;
using namespace std;
 
// This is a complete proof of the existence of 3 different
// periodic solution for the Rossler system
// with chaotic parameter values a=5.7, b=0.2
 
// ---------------------------------------------------------------------
// The following function computes the Interval Newton Operator for the function
//   f(x) = P^period(x)-x
// on the set X.
// Then it verifies existence and uniqueness of a periodic point in the set set X.
// Parameters are:
// @param pm - an instance of PoincareMap for the Rossler system
// @param X - 2-dimensional interval vector in which we want to prove the existence of an unique periodic point
// @param period - is a period of the point for the Poincare map
 
void verifyExistenceOfPeriodicOrbit(IPoincareMap& pm, IVector X, int period)
{
  IVector center = midVector(X);
  interval returnTime;
 
  // Center is 2-dimensional. Embed it into Poincare section, i.e. add first coordinate x=0.
  // Define a tripleton representation of the center of X.
  C0HOTripletonSet s1({interval(0.),center[0],center[1]});
 
  // Compute iteration of Poincare map at the center (3-dim object is returned).
  IVector y = pm(s1,returnTime,period);
 
  // Project it onto 2-dim Poincare section, first coordinate is ignored.
  IVector imCenter(2,y.begin()+1);
 
 
  // Derivative of PM on the set X.
  // Define doubleton representation of the first order variational equations.
  C1HORect2Set s2({interval(0.),X[0],X[1]});
 
  // The matrix monodromyMatrix will store derivatives of the FLOW not Poincare map.
  IMatrix monodromyMatrix(3,3);
  y = pm(s2,monodromyMatrix,returnTime,period);
 
  // This member function recomputes derivatives of the flow into derivatives of Poincare map
  IMatrix DP = pm.computeDP(y,monodromyMatrix);
 
  // We extract a 2x2 slice from 3x3 DP matrix and subtract identity.
  IMatrix DP_Minus_Id(2,2);
  DP_Minus_Id[0][0] = DP[1][1] - 1.;
  DP_Minus_Id[0][1] = DP[1][2];
  DP_Minus_Id[1][0] = DP[2][1];
  DP_Minus_Id[1][1] = DP[2][2] - 1.;
  interval d = DP[1][1]*DP[2][2]-DP[1][2]*DP[2][1];
  interval tr = DP[1][1] + DP[2][2]; 
  interval s = sqrt(sqr(tr)-4*d);
  // Compute interval Newton operator.
  IVector N = center - capd::matrixAlgorithms::gauss(DP_Minus_Id,imCenter-center);
 
  // Verification if N is a subset of X
  cout << "\n---------------------------------------------------\n\nN = " << N << endl;
  cout << "X = " << X << endl;
  cout << "Return time: " << returnTime << endl;
  cout << "ev1=" << (tr-s)/2 << ", ev2=" << (tr+s)/2 << endl;
  if(subsetInterior(N,X))
    cout << "the existence of period " << period << " orbit verified\n";
  else
  {
    cout << "N is not a subset of X\n\n";
    cout << "diam(N)=" << diam(N) << endl;
    cout << "diam(X)=" << diam(X) << endl;
    cout << "N-X" << N-X << endl;
  }
}
 
// ----------------------------------- MAIN ----------------------------------------
 
int main()
{
  cout.precision(17);
  try{
// Define vector field, ODE solver and Poincare map for the Rossler system.
    IMap vf("par:a,b;var:x,y,z;fun:-(y+z),x+b*y,b+z*(x-a);");
    vf.setParameter("a", interval(57)/interval(10));
    vf.setParameter("b", interval(2)/interval(10));
 
    int order = 30;
    IOdeSolver solver(vf, order);
    ICoordinateSection section(3, 0); // the Poincare section is x=0, i.e. index 0 of 3
    IPoincareMap pm(solver, section, poincare::MinusPlus);
 
 
// For all the orbits below the radius of ball in max norm in which we verify the existence of an unique orbit is set to:
    double s = 4e-13;
    IVector center(2), box(2);
    box[0] = s*interval(-1,1);
    box[1] = s*interval(-1,1);
    cout << "Define a box X of diameter " << 2.*s << " around each candidate for p.o. and compute Interval Newton Operator N"  << endl;
 
// fixed point
    center[0] = -8.3809417428298;
    center[1] = 0.029590060630665;
    verifyExistenceOfPeriodicOrbit(pm,center+box,1);
 
// period 2 orbit
    center[0] = -5.4240738226652;
    center[1] = 0.031081210807875;
    verifyExistenceOfPeriodicOrbit(pm,center+box,2);
 
// period 3 orbit
    center[0] = -6.233158628537965;
    center[1] = 0.03064011165815;
    verifyExistenceOfPeriodicOrbit(pm,center+box,3);
 
   }catch(exception& e)
  {
    cout << "\n\nException caught: "<< e.what() << endl;
  }
  return 0;
}
 
/* output:
Define a box X of diameter 8.0000000000000002e-13 around each candidate for p.o. and compute Interval Newton Operator N
 
---------------------------------------------------
 
N = {[-8.3809417428299415, -8.3809417428298101],[0.029590060630665858, 0.029590060630668349]}
X = {[-8.3809417428302009, -8.380941742829398],[0.029590060630264998, 0.029590060631065004]}
Return time: [5.8810884555537228, 5.881088455554079]
the existence of period 1 orbit verified
 
---------------------------------------------------
 
N = {[-5.4240738226653775, -5.4240738226650347],[0.031081210807869089, 0.031081210807883793]}
X = {[-5.4240738226656005, -5.4240738226647993],[0.031081210807474998, 0.031081210808275004]}
Return time: [11.758626071659574, 11.758626071660617]
the existence of period 2 orbit verified
 
---------------------------------------------------
 
N = {[-6.2331586285383187, -6.2331586285376348],[0.030640111658149713, 0.030640111658171425]}
X = {[-6.2331586285383658, -6.2331586285375646],[0.030640111657749998, 0.030640111658550004]}
Return time: [17.515791070334913, 17.515791070336615]
the existence of period 3 orbit verified
*/
 
// END