Classes
class	C0DoubletonSetGeometricTail

class	C0HODoubletonSetGeometricTail
	This class uses representation of subset of R^n inherited from template parameter. More...

class	C1DoubletonSetGeometricTail

struct	ComputeOneStepSectionEnclosure

struct	ComputeOneStepSectionEnclosure< false >

class	DissipativeVectorField
	The class provides a common interface for a dissipative vector required by the class PdeSolver. More...

class	GeometricBound
	The class is class represents a subset of a countable infinite dimensional space. More...

class	OneDimKSSineVectorField
	The class implements vector field of the one-dimensional real Kuramoto-Shivashinsky PDE under the following assumptions 1 .The solutions are represented in the Fourier basis. More...

class	PdeAbstractSection

class	PdeAffineSection
	TimeMap class provides class that serves as an affine Poincare section. More...

class	PdeCoordinateSection
	TimeMap class provides class that serves as Poincare section of the form x_i = c. More...

class	PdeCurve
	This class is a data structure for storing of a parametric curve together with first order derivatives with respect to initial point. More...

struct	PdeSectionDerivativesEnclosure

class	PdeSolver

class	PolyLogBound
	The class is class represents a subset of a countable infinite dimensional space. More...

class	PolynomialBound

Functions
GeometricBound	operator+ (const GeometricBound &x, const GeometricBound &y)
	operator+ More...

GeometricBound	operator- (const GeometricBound &x, const GeometricBound &y)
	operator- More...

GeometricBound	operator* (const interval &s, const GeometricBound &x)
	operator* More...

GeometricBound	operator* (const GeometricBound &x, const interval &s)
	operator* More...

GeometricBound	operator* (const IMatrix &A, const GeometricBound &v)
	This operator realizes the following Matrix by vector multiplication (AmainVariables,Idtail) More...

std::ostream &	operator<< (std::ostream &s, const GeometricBound &x)
	operator<< More...

void	split (const GeometricBound &X, GeometricBound &x, GeometricBound &dx)

GeometricBound	intersection (const GeometricBound &x, const GeometricBound &y)

GeometricBound	midVector (const GeometricBound &x)

void	swap (GeometricBound &a, GeometricBound &b)

PolyLogBound	operator+ (const PolyLogBound &x, const PolyLogBound &y)
	operator+ More...

PolyLogBound	operator- (const PolyLogBound &x, const PolyLogBound &y)
	operator- More...

PolyLogBound	operator* (const interval &s, const PolyLogBound &x)
	operator* More...

PolyLogBound	operator* (const PolyLogBound &x, const interval &s)
	operator* More...

PolyLogBound	operator* (const IMatrix &A, const PolyLogBound &x)
	operator* More...

std::ostream &	operator<< (std::ostream &s, const PolyLogBound &x)
	operator<< More...

PolyLogBound	intersection (const PolyLogBound &x, const PolyLogBound &y)

void	split (const PolyLogBound &X, PolyLogBound &x, PolyLogBound &dx)

PolyLogBound	midVector (const PolyLogBound &x)

template<typename Scalar , typename Exponent , int M>
PolynomialBound< Scalar, Exponent, M >	operator+ (const PolynomialBound< Scalar, Exponent, M > &x, const PolynomialBound< Scalar, Exponent, M > &y)
	this operator realizes addition of two PolynomialBounds More...

template<typename Scalar , typename Exponent , int M>
PolynomialBound< Scalar, Exponent, M >	operator- (const PolynomialBound< Scalar, Exponent, M > &v1, const PolynomialBound< Scalar, Exponent, M > &v2)
	this operator realizes subtraction of two PolynomialBounds More...

template<typename Scalar , typename Exponent , int M>
PolynomialBound< Scalar, Exponent, M >	operator* (const Scalar &s, const PolynomialBound< Scalar, Exponent, M > &v)
	this operator realizes multiplication of any coefficient in PolynomialBound by some scalar More...

template<typename Scalar , typename Exponent , int M>
PolynomialBound< Scalar, Exponent, M >	operator* (const PolynomialBound< Scalar, Exponent, M > &p, const Scalar &s)
	this operator realizes multiplication of any coefficient in PolynomialBound by some scalar More...

template<typename Scalar , typename Exponent , int M, int dim>
PolynomialBound< Scalar, Exponent, M >	operator* (const capd::vectalg::Matrix< Scalar, dim, dim > &A, const PolynomialBound< Scalar, Exponent, M > &p)
	this operator realizes change of coordiante on some PolynomialBound More...

template<typename Scalar , typename Exponent , int M>
std::ostream &	operator<< (std::ostream &s, const PolynomialBound< Scalar, Exponent, M > &p)
	this operator writes a PolynomialBound object to a given stream in the following form {{p_1,p_2,...,p_M},C,exponent} where M is a number of main coefficients in an object p More...

template<typename Scalar , typename Exponent , int M>
PolynomialBound< Scalar, Exponent, M >	computeQF (const PolynomialBound< Scalar, Exponent, M > &y, const PolynomialBound< Scalar, Exponent, M > &w)
	the function computes value of operator QF on two PolynomialBounds y and w given by QF_i = 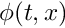$\sum_{k=1}^{i-1} y_k w_{i-k}$ More...

template<typename Scalar , typename Exponent , int M>
PolynomialBound< Scalar, Exponent, M >	computeQI (const PolynomialBound< Scalar, Exponent, M > &y, const PolynomialBound< Scalar, Exponent, M > &w)
	the function computes value of operator QI on two PolynomialBounds y and w given by QI_i = 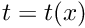$\sum_{k=1}^\infty y_k w_{k+i}$ More...

Function Documentation

◆ computeQF()

template<typename Scalar , typename Exponent , int M>

PolynomialBound< Scalar, Exponent, M > capd::pdes::computeQF	(	const PolynomialBound< Scalar, Exponent, M > &	y,
		const PolynomialBound< Scalar, Exponent, M > &	w
	)

the function computes value of operator QF on two PolynomialBounds y and w given by QF_i = 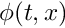$\sum_{k=1}^{i-1} y_k w_{i-k}$

Parameters

[in]	y	object of class PolynomialBound
[in]	w	object of class PolynomialBound

Returns: value of operator QF on polynomial bounds y and w

◆ computeQI()

template<typename Scalar , typename Exponent , int M>

PolynomialBound< Scalar, Exponent, M > capd::pdes::computeQI	(	const PolynomialBound< Scalar, Exponent, M > &	y,
		const PolynomialBound< Scalar, Exponent, M > &	w
	)

the function computes value of operator QI on two PolynomialBounds y and w given by QI_i = 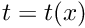$\sum_{k=1}^\infty y_k w_{k+i}$

Parameters

[in]	y	object of class PolynomialBound
[in]	w	object of class PolynomialBound

Returns: value of operator QI on polynomial bounds y and w

◆ intersection() [1/2]

GeometricBound capd::pdes::intersection	(	const GeometricBound &	x,
		const GeometricBound &	y
	)

◆ intersection() [2/2]

PolyLogBound capd::pdes::intersection	(	const PolyLogBound &	x,
		const PolyLogBound &	y
	)

◆ midVector() [1/2]

GeometricBound capd::pdes::midVector ( const GeometricBound & x )

inline

◆ midVector() [2/2]

PolyLogBound capd::pdes::midVector ( const PolyLogBound & x )

inline

◆ operator*() [1/9]

template<typename Scalar , typename Exponent , int M, int dim>

PolynomialBound< Scalar, Exponent, M > capd::pdes::operator*	(	const capd::vectalg::Matrix< Scalar, dim, dim > &	A,
		const PolynomialBound< Scalar, Exponent, M > &	p
	)

this operator realizes change of coordiante on some PolynomialBound

if A is m\times m martix then the first m coordinates of result are given by result_i = 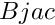$\sum_{k=1}^m A_{i,k} p_k$ on the other coefficients change of coordinates is identity

Parameters

[in]	A	square matrix of dimension smaller than p.dimension()
[in]	p	object of class PolynomialBound

Returns: PolynomialBound p in new coordinate system

◆ operator*() [2/9]

GeometricBound capd::pdes::operator*	(	const GeometricBound &	x,
		const interval &	s
	)

operator*

this operator realizes multiplication of any coefficient in a GeometricBound by some scalar

using the following formula result_i = s * x_i

Parameters

[in]	s	object of type Scalar
[in]	x	object of class GeometricBound

Returns: GeometricBound x multiplied by s

◆ operator*() [3/9]

GeometricBound capd::pdes::operator*	(	const IMatrix &	A,
		const GeometricBound &	x
	)

This operator realizes the following Matrix by vector multiplication (A*mainVariables,Id*tail)

operator*

this operator realizes linear transformation of a GeometricBound

if A is square matrix m\times m then the first m coordinates of result are given by 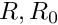$result_i = \sum_{k=1}^m A_{i,k} x_k$ The remaining (infinite number) of coordinates remain unchanged.

Parameters

[in]	A	square matrix of dimension smaller than p.dimension()
[in]	x	object of class GeometricBound

Returns: GeometricBound x in transformed by (A,Id)

Note: The dimension m of the matrix A must be less or equal than number of exactly represented coefficients in x. Exception is thrown if this requirement is violated.

◆ operator*() [4/9]

PolyLogBound capd::pdes::operator*	(	const IMatrix &	A,
		const PolyLogBound &	x
	)

operator*

this operator realizes linear transformation of a PolyLogBound

if A is square matrix m\times m then the first m coordinates of result are given by 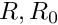$result_i = \sum_{k=1}^m A_{i,k} x_k$ The remaining (infinite number) of coordinates remain unchanged.

Parameters

[in]	A	square matrix of dimension smaller than p.dimension()
[in]	x	object of class PolyLogBound

Returns: PolyLogBound x in transformed by (A,Id)

Note: The dimension m of the matrix A must be less or equal than number of exactly represented coefficients in x. Exception is thrown if this requirement is violated.

◆ operator*() [5/9]

GeometricBound capd::pdes::operator*	(	const interval &	s,
		const GeometricBound &	x
	)

operator*

this operator realizes multiplication of any coefficient in a GeometricBound by some scalar

using the following formula result_i = s * x

Parameters

[in]	s	object of type Scalar
[in]	x	object of class GeometricBound

Returns: GeometricBound p multiplied by s

◆ operator*() [6/9]

PolyLogBound capd::pdes::operator*	(	const interval &	s,
		const PolyLogBound &	x
	)

operator*

this operator realizes multiplication of any coefficient in a PolyLogBound by some scalar

using the following formula result_i = s * x

Parameters

[in]	s	object of type Scalar
[in]	x	object of class PolyLogBound

Returns: PolyLogBound p multiplied by s

◆ operator*() [7/9]

PolyLogBound capd::pdes::operator*	(	const PolyLogBound &	x,
		const interval &	s
	)

operator*

this operator realizes multiplication of any coefficient in a PolyLogBound by some scalar

using the following formula result_i = s * x_i

Parameters

[in]	s	object of type Scalar
[in]	x	object of class PolyLogBound

Returns: PolyLogBound x multiplied by s

◆ operator*() [8/9]

template<typename Scalar , typename Exponent , int M>

PolynomialBound< Scalar, Exponent, M > capd::pdes::operator*	(	const PolynomialBound< Scalar, Exponent, M > &	p,
		const Scalar &	s
	)

this operator realizes multiplication of any coefficient in PolynomialBound by some scalar

using the following formula result_i = s * p_i

Parameters

[in]	p	object of class PolynomialBound
[in]	s	object of type Scalar

Returns: PolynomialBound p multiplied by s

◆ operator*() [9/9]

template<typename Scalar , typename Exponent , int M>

PolynomialBound< Scalar, Exponent, M > capd::pdes::operator*	(	const Scalar &	s,
		const PolynomialBound< Scalar, Exponent, M > &	v
	)

this operator realizes multiplication of any coefficient in PolynomialBound by some scalar

using the following formula result_i = s * p_i

Parameters

[in]	s	object of type Scalar
[in]	p	object of class PolynomialBound

Returns: PolynomialBound p multiplied by s

◆ operator+() [1/3]

GeometricBound capd::pdes::operator+	(	const GeometricBound &	x,
		const GeometricBound &	y
	)

operator+

this operator realizes addition of two GeometricBound using the following formula result_i = x_i + y_i Since object is represented as a finite dimensional vector and a tail we do explicit summation on main variables only. Exponent of result is computed as t = min(x.exponent(),y.exponent())

The constant used in representation of tail in result is computed as M = M_result = min(M_x,M_y) - number of exactly represented coefficients C_result = C_x/(M+1)^{x.exponent()-t} + C_y/(M+1)^{y.exponent()-t}

Parameters

[in]	x	object of class GeometricBound
[in]	y	object of class GeometricBound

Returns: sum of x and y

◆ operator+() [2/3]

PolyLogBound capd::pdes::operator+	(	const PolyLogBound &	x,
		const PolyLogBound &	y
	)

operator+

this operator realizes addition of two PolyLogBound using the following formula result_i = x_i + y_i Since object is represented as a finite dimensional vector and a tail we do explicit summation on main variables only. Exponent of result is computed as t = min(x.exponent(),y.exponent())

The constant used in representation of tail in result is computed as M = M_result = min(M_x,M_y) - number of exactly represented coefficients C_result = C_x/(M+1)^{x.exponent()-t} + C_y/(M+1)^{y.exponent()-t}

Parameters

[in]	x	object of class PolyLogBound
[in]	y	object of class PolyLogBound

Returns: sum of x and y

◆ operator+() [3/3]

template<typename Scalar , typename Exponent , int M>

PolynomialBound< Scalar, Exponent, M > capd::pdes::operator+	(	const PolynomialBound< Scalar, Exponent, M > &	x,
		const PolynomialBound< Scalar, Exponent, M > &	y
	)

this operator realizes addition of two PolynomialBounds

using the following formula result_i = x_i + y_i Since object is represented as a finite dimensional vector and a tail we do explicit summation on main variables only. Exponent of result is computed as t = min(x.exponent(),y.exponent()) The constant used in representation of tail in result is computed as C_result = C_x/(M+1)^{x.exponent()-t} + C_y/(M+1)^{y.exponent()-t}

Parameters

[in]	x	object of class PolynomialBound
[in]	y	object of class PolynomialBound

Returns: sum of x and y

◆ operator-() [1/3]

GeometricBound capd::pdes::operator-	(	const GeometricBound &	x,
		const GeometricBound &	y
	)

operator-

this operator realizes subtraction of two GeometricBound using the following formula result_i = x_i - y_i Since object is represented as a finite dimensional vector and a tail we do explicit summation on main variables only. Exponent of result is computed as t = min(x.exponent(),y.exponent())

The constant used in representation of tail in result is computed as M = M_result = min(M_x,M_y) - number of exactly represented coefficients C_result = C_x/(M+1)^{x.exponent()-t} + C_y/(M+1)^{y.exponent()-t}

Parameters

[in]	x	object of class GeometricBound
[in]	y	object of class GeometricBound

Returns: subtraction of x and y

◆ operator-() [2/3]

PolyLogBound capd::pdes::operator-	(	const PolyLogBound &	x,
		const PolyLogBound &	y
	)

operator-

this operator realizes subtraction of two PolyLogBound using the following formula result_i = x_i - y_i Since object is represented as a finite dimensional vector and a tail we do explicit summation on main variables only. Exponent of result is computed as t = min(x.exponent(),y.exponent())

The constant used in representation of tail in result is computed as M = M_result = min(M_x,M_y) - number of exactly represented coefficients C_result = C_x/(M+1)^{x.exponent()-t} + C_y/(M+1)^{y.exponent()-t}

Parameters

[in]	x	object of class PolyLogBound
[in]	y	object of class PolyLogBound

Returns: subtraction of x and y

◆ operator-() [3/3]

template<typename Scalar , typename Exponent , int M>

PolynomialBound< Scalar, Exponent, M > capd::pdes::operator-	(	const PolynomialBound< Scalar, Exponent, M > &	v1,
		const PolynomialBound< Scalar, Exponent, M > &	v2
	)

this operator realizes subtraction of two PolynomialBounds

using the following formula result_i = x_i - y_i Since object is represented as a finite dimensional vector and a tail we do explicit subtraction on main variables only. Exponent of result is computed as t = min(x.exponent(),y.exponent()) The constant used in representation of tail in result is computed as C_result = C_x/(M+1)^{x.exponent()-t} + C_y/(M+1)^{y.exponent()-t}

Parameters

[in]	x	object of class PolynomialBound
[in]	y	object of class PolynomialBound

Returns: difference of x and y

◆ operator<<() [1/3]

std::ostream & capd::pdes::operator<<	(	std::ostream &	s,
		const GeometricBound &	x
	)

operator<<

This operator writes a GeometricBound object to a given stream in the following form {{x_1,x_2,...,x_M},C,exponent} where M is the number of exactly represented coefficients of x.

Parameters

[in]	out	- a stream to which the object x is to be written
[in]	x	- an instance of class GeometricBound

Returns: a reference to stream out

◆ operator<<() [2/3]

std::ostream& capd::pdes::operator<<	(	std::ostream &	s,
		const PolyLogBound &	x
	)

operator<<

This operator writes a PolyLogBound object to a given stream in the following form {{x_1,x_2,...,x_M},C,exponent} where M is the number of exactly represented coefficients of x.

Parameters

[in]	out	- a stream to which the object x is to be written
[in]	x	- an instance of class PolyLogBound

Returns: a reference to stream out

◆ operator<<() [3/3]

template<typename Scalar , typename Exponent , int M>

std::ostream & capd::pdes::operator<<	(	std::ostream &	s,
		const PolynomialBound< Scalar, Exponent, M > &	p
	)

this operator writes a PolynomialBound object to a given stream in the following form {{p_1,p_2,...,p_M},C,exponent} where M is a number of main coefficients in an object p

Parameters

[in]	s	a stream to which object p is printed
[in]	p	object of class PolynomialBound

Returns: a reference to stream s

◆ split() [1/2]

void capd::pdes::split	(	const GeometricBound &	X,
		GeometricBound &	x,
		GeometricBound &	dx
	)

◆ split() [2/2]

void capd::pdes::split	(	const PolyLogBound &	X,
		PolyLogBound &	x,
		PolyLogBound &	dx
	)

◆ swap()

void capd::pdes::swap	(	GeometricBound &	a,
		GeometricBound &	b
	)

inline

Classes

Functions

Function Documentation

◆ computeQF()

◆ computeQI()

◆ intersection() [1/2]

◆ intersection() [2/2]

◆ midVector() [1/2]

◆ midVector() [2/2]

◆ operator*() [1/9]

◆ operator*() [2/9]

◆ operator*() [3/9]

◆ operator*() [4/9]

◆ operator*() [5/9]

◆ operator*() [6/9]

◆ operator*() [7/9]

◆ operator*() [8/9]

◆ operator*() [9/9]

◆ operator+() [1/3]

◆ operator+() [2/3]

◆ operator+() [3/3]

◆ operator-() [1/3]

◆ operator-() [2/3]

◆ operator-() [3/3]

◆ operator<<() [1/3]

◆ operator<<() [2/3]

◆ operator<<() [3/3]

◆ split() [1/2]

◆ split() [2/2]

◆ swap()