The class implements vector field of the one-dimensional real Kuramoto-Shivashinsky PDE under the following assumptions 1 .The solutions are represented in the Fourier basis. More...

#include <capd/pdes/OneDimKSSineVectorField.h>

Public Types
typedef capd::interval	ScalarType

typedef capd::pdes::GeometricBound	VectorType

typedef capd::IMatrix	MatrixType

typedef capd::IVector::size_type	size_type

typedef std::vector< VectorType >	VectorArray

typedef std::vector< VectorArray >	MatrixArray

typedef std::vector< ScalarType >	ScalarArray

typedef std::pair< VectorArray , VectorArray >	C1Data

typedef MatrixType::RowVectorType	FiniteVectorType

Public Member Functions
	OneDimKSSineVectorField (ScalarType nu, size_type dim, size_type firstDissipativeVariable)
	constructs vector field of KS-equation. More...

VectorType	operator() (ScalarType h, const VectorType &v)

VectorType	operator() (ScalarType h, const VectorType &v, MatrixType &A)

MatrixType	derivative (ScalarType h, const VectorType &v)
	this method computes finite-dimensional square block of the derivative of the vector field More...

void	derivative (ScalarType h, const VectorType &v, MatrixType &A, ScalarType &Dxy, ScalarType &Dyx, ScalarType &Dyy)
	This method computed bounds on the derivative of vector field. The finite-dimensional block is computed explicitely, Operator norm of three infinite-dimensional blocks is bounded and returned. More...

void	computeODECoefficients (VectorArray &a, size_type order)
	computes Taylor coefficients for C^0 part More...

void	computeODECoefficients (const VectorArray &a, VectorArray &c, size_type order)
	given coefficients for C^0 part, it computes Taylor coefficient for variational equation (one column) with initial condition 'c' More...

void	makeSelfConsistentBound (VectorArray &a)
	This function should refine the tail so that the vector field is pointing inwards the tail. More...

void	makeSelfConsistentBound (VectorArray &a, MatrixArray &J1, MatrixArray &J2, size_type numberOfColumns)
	This function should refine the tail so that the vector field for variational equation is pointing inwards the tail. Here we assume two different initial conditions J1=(Id,0) and J2=(0,something) More...

size_type	dimension () const

size_type	firstDissipativeIndex () const

void	updateTail (VectorType &x, const VectorArray &enc, ScalarType h) const
	Update tail for C^0 part using linear differential inequality. More...

void	updateTail (VectorArray &DyxId, VectorArray &Dyx, const MatrixArray &Enc, const MatrixArray &DyxEnc, ScalarType h) const
	Update tail for two C^1 blocks using linear differential inequality. More...

MatrixType	blockNorms (const VectorType &a, size_type m) const
	This function should compute a matrix M such that M_ii is logarithmic norm of the diagonal block M_ij is a norm of ij block The infinite dimensional space is split onto m+1 blocks. More...

ScalarType	getLambda (size_type k)

void	computeODECoefficients (VectorArray &a, MatrixArray &J, size_type p, size_type numberOfColumns)
	This function should compute ODE coefficients up to given order at the set a Moreover, block derivative of first group of variables has to be computed. More...

virtual size_type	dimension () const=0

virtual size_type	firstDissipativeIndex () const=0

Public Attributes
ScalarType	nu

size_type	m_dimension

size_type	m_firstDissipativeVariable

ScalarArray	lambda

ScalarArray	nonlinearPart

std::vector< ScalarArray >	jacNonlinearPart

std::vector< ScalarArray >	dyxNonlinearPart

Detailed Description

The class implements vector field of the one-dimensional real Kuramoto-Shivashinsky PDE under the following assumptions 1 .The solutions are represented in the Fourier basis.

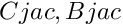
We impose periodic and odd solutions, thus only sine components are present. The functions are represented as $u(t,x) = -2 \sum_{k=1}^\infty a_k(t) \sin (ikx)$
Domain is restricted to some subset of analytic functions. We impose geometric-like decay of Fourier coefficients. |a_k| < C/(q^k k^s), for some real constants q>1 and s

The implementation provides

evaluation of vector field on a representable set of analytic functions
computation of partial derivatives of the vector field with respect to finite number of variables
automatic differentiation for d/dt^i, i-natural number
automatic differentiation for d/da_k dt^i - -natural number k-bounded

Member Typedef Documentation

◆ C1Data

typedef std::pair<VectorArray*, VectorArray*> capd::pdes::OneDimKSSineVectorField::C1Data

◆ FiniteVectorType

typedef MatrixType::RowVectorType capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >::FiniteVectorType

inherited

◆ MatrixArray

typedef std::vector<VectorArray> capd::pdes::OneDimKSSineVectorField::MatrixArray

◆ MatrixType

typedef capd::IMatrix capd::pdes::OneDimKSSineVectorField::MatrixType

◆ ScalarArray

typedef std::vector<ScalarType> capd::pdes::OneDimKSSineVectorField::ScalarArray

◆ ScalarType

typedef capd::interval capd::pdes::OneDimKSSineVectorField::ScalarType

◆ size_type

typedef capd::IVector::size_type capd::pdes::OneDimKSSineVectorField::size_type

◆ VectorArray

typedef std::vector<VectorType> capd::pdes::OneDimKSSineVectorField::VectorArray

◆ VectorType

typedef capd::pdes::GeometricBound capd::pdes::OneDimKSSineVectorField::VectorType

Constructor & Destructor Documentation

◆ OneDimKSSineVectorField()

capd::pdes::OneDimKSSineVectorField::OneDimKSSineVectorField	(	ScalarType	nu,
		size_type	dim,
		size_type	firstDissipativeVariable
	)

constructs vector field of KS-equation.

Parameters

[in] nu - viscosity parameter in the KS-equation

Member Function Documentation

◆ blockNorms()

MatrixType capd::pdes::OneDimKSSineVectorField::blockNorms	(	const VectorType &	a,
		size_type	m
	)		const

inlinevirtual

This function should compute a matrix M such that M_ii is logarithmic norm of the diagonal block M_ij is a norm of ij block The infinite dimensional space is split onto m+1 blocks.

Implements capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >.

◆ computeODECoefficients() [1/3]

void capd::pdes::OneDimKSSineVectorField::computeODECoefficients	(	const VectorArray &	a,
		VectorArray &	c,
		size_type	order
	)

virtual

given coefficients for C^0 part, it computes Taylor coefficient for variational equation (one column) with initial condition 'c'

Implements capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >.

◆ computeODECoefficients() [2/3]

void capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >::computeODECoefficients	(	VectorArray &	a,
		MatrixArray &	J,
		size_type	p,
		size_type	numberOfColumns
	)

inlineinherited

This function should compute ODE coefficients up to given order at the set a Moreover, block derivative of first group of variables has to be computed.

◆ computeODECoefficients() [3/3]

void capd::pdes::OneDimKSSineVectorField::computeODECoefficients	(	VectorArray &	a,
		size_type	order
	)

virtual

computes Taylor coefficients for C^0 part

Implements capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >.

◆ derivative() [1/2]

MatrixType capd::pdes::OneDimKSSineVectorField::derivative	(	ScalarType	h,
		const VectorType &	v
	)

inlinevirtual

this method computes finite-dimensional square block of the derivative of the vector field

Implements capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >.

◆ derivative() [2/2]

void capd::pdes::OneDimKSSineVectorField::derivative	(	ScalarType	h,
		const VectorType &	v,
		MatrixType &	A,
		ScalarType &	Dxy,
		ScalarType &	Dyx,
		ScalarType &	Dyy
	)

inline

This method computed bounds on the derivative of vector field. The finite-dimensional block is computed explicitely, Operator norm of three infinite-dimensional blocks is bounded and returned.

now we have to estimate three norms

◆ dimension() [1/2]

size_type capd::pdes::OneDimKSSineVectorField::dimension ( ) const

inline

◆ dimension() [2/2]

virtual size_type capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >::dimension

pure virtualinherited

◆ firstDissipativeIndex() [1/2]

size_type capd::pdes::OneDimKSSineVectorField::firstDissipativeIndex ( ) const

inline

◆ firstDissipativeIndex() [2/2]

virtual size_type capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >::firstDissipativeIndex

pure virtualinherited

◆ getLambda()

ScalarType capd::pdes::OneDimKSSineVectorField::getLambda ( size_type k )

inline

◆ makeSelfConsistentBound() [1/2]

void capd::pdes::OneDimKSSineVectorField::makeSelfConsistentBound ( VectorArray & a )

inlinevirtual

This function should refine the tail so that the vector field is pointing inwards the tail.

Implements capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >.

◆ makeSelfConsistentBound() [2/2]

void capd::pdes::OneDimKSSineVectorField::makeSelfConsistentBound	(	VectorArray &	a,
		MatrixArray &	J1,
		MatrixArray &	J2,
		size_type	numberOfColumns
	)

virtual

This function should refine the tail so that the vector field for variational equation is pointing inwards the tail. Here we assume two different initial conditions J1=(Id,0) and J2=(0,something)

Implements capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >.

◆ operator()() [1/2]

VectorType capd::pdes::OneDimKSSineVectorField::operator()	(	ScalarType	h,
		const VectorType &	v
	)

inlinevirtual

Implements capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >.

◆ operator()() [2/2]

VectorType capd::pdes::OneDimKSSineVectorField::operator()	(	ScalarType	h,
		const VectorType &	v,
		MatrixType &	A
	)

inlinevirtual

Implements capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >.

◆ updateTail() [1/2]

void capd::pdes::OneDimKSSineVectorField::updateTail	(	VectorArray &	DyxId,
		VectorArray &	Dyx,
		const MatrixArray &	Enc,
		const MatrixArray &	DyxEnc,
		ScalarType	h
	)		const

inlinevirtual

Update tail for two C^1 blocks using linear differential inequality.

Implements capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >.

◆ updateTail() [2/2]

void capd::pdes::OneDimKSSineVectorField::updateTail	(	VectorType &	x,
		const VectorArray &	enc,
		ScalarType	h
	)		const

inlinevirtual

Update tail for C^0 part using linear differential inequality.

Implements capd::pdes::DissipativeVectorField< capd::pdes::GeometricBound >.

Member Data Documentation

◆ dyxNonlinearPart

std::vector<ScalarArray> capd::pdes::OneDimKSSineVectorField::dyxNonlinearPart

◆ jacNonlinearPart

std::vector<ScalarArray> capd::pdes::OneDimKSSineVectorField::jacNonlinearPart

◆ lambda

ScalarArray capd::pdes::OneDimKSSineVectorField::lambda

◆ m_dimension

size_type capd::pdes::OneDimKSSineVectorField::m_dimension

◆ m_firstDissipativeVariable

size_type capd::pdes::OneDimKSSineVectorField::m_firstDissipativeVariable

◆ nonlinearPart

ScalarArray capd::pdes::OneDimKSSineVectorField::nonlinearPart

◆ nu

ScalarType capd::pdes::OneDimKSSineVectorField::nu

Public Types

Public Member Functions

Public Attributes

Detailed Description

Member Typedef Documentation

◆ C1Data

◆ FiniteVectorType

◆ MatrixArray

◆ MatrixType

◆ ScalarArray

◆ ScalarType

◆ size_type

◆ VectorArray

◆ VectorType

Constructor & Destructor Documentation

◆ OneDimKSSineVectorField()

Member Function Documentation

◆ blockNorms()

◆ computeODECoefficients() [1/3]

◆ computeODECoefficients() [2/3]

◆ computeODECoefficients() [3/3]

◆ derivative() [1/2]

◆ derivative() [2/2]

◆ dimension() [1/2]

◆ dimension() [2/2]

◆ firstDissipativeIndex() [1/2]

◆ firstDissipativeIndex() [2/2]

◆ getLambda()

◆ makeSelfConsistentBound() [1/2]

◆ makeSelfConsistentBound() [2/2]

◆ operator()() [1/2]

◆ operator()() [2/2]

◆ updateTail() [1/2]

◆ updateTail() [2/2]

Member Data Documentation

◆ dyxNonlinearPart

◆ jacNonlinearPart

◆ lambda

◆ m_dimension

◆ m_firstDissipativeVariable

◆ nonlinearPart

◆ nu