Accepted input

RedHom computes homology of

• Cubical sets, which are finite unions of Cartesian products of elementary cubes I₁ x I₂ x ... x I_d of d closed intervals I_i=[a_i,b_i] with integer endpoints a_i,b_i satisfying a_i=b_i (degenerate interval) or a_i+1=b_i (nondegenerate interval).
• Full cubical sets, which are as above but allow only nondegenerate intervals in the Cartesian product.
• Polyhedra represented as abstract or geometric simplicial complexes
• Regular CW complexes

Data format for cubical sets

A cubical set is represented as a list of elementary cubes enclosed in braces and separated by commas. Each elementary cube is written as a Cartesian product of intervals with lower case letter x standing for the cross product. Intervals are enclosed in brackets and their coorinates are separated by commas.

A sample text file, representing cubical sphere embedded in R² is as follows:
{
[0,1]x[0],
[1]x[-1,0],
[0,1]x[-1],
[0]x[-1,0]
}
We recommend the file extension *.pcub for files storing cubical sets in this format. To indicate that data format provided to redHom use the command line option --fileType pcub or shortly -f pcub. Sample file containing cubical torus can be found here.

Data format for full cubical sets

A full cubical set is represented as a newline separated list of the lower coordinates of each interval in the Cartesian product representation of an elementary cube. The coordinates may be enclosed in parentheses and seperated by commas.

The full cubical sphere embedded in R² is represented in this format as follows:

fcub:	Illustration:
(1,1) (2,1) (3,1) (1,2) (3,2) (1,3) (2,3) (3,3)

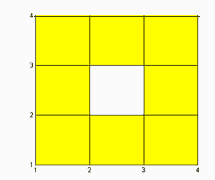
W recommend the extension *.fcub for full cubical sets stored in such format. Sample file containing cubical Klein bottle represented as a full cubical set is here. To indicate that data format provided to redHom use the command line option --fileType fcub or simply -f fcub.

Data format for simplicial complexes

The simplicial complex is given as the list of its maximal simplices and each simplex is represented as the list of the integer labels of vertices. We recommend the file extension *.dat for files in this format. This data format may be forced by using redhom program with the -f dat option.

A special case of the well-know obj format used in 3D graphiscs is also accepted. See here for the detailed description of the format. The recommended extension for this data format is *.obj. This data format may be forced by using redhom program with the -f dat option.

An example of a simplicial complex with its representation in the two formats is presented below. The file containting the example in the *.dat format is available here and in the *.obj format here.

dat:	obj:	Illustration:
1 2 2 3 4 4 1 1 5 4 5 1 6	v 5 4 v 3 5 v 1 3 v 2 1 v 6 2 v 7 3 f 1 2 f 2 3 4 f 4 1 f 1 5 f 4 5 f 1 6

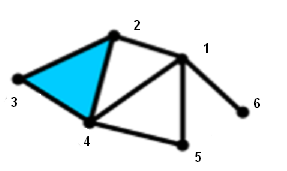
Data format for acyclic valued, upper semicontinuous cubical maps

An acyclic valued cubical map from a full cubical set X to itself assigns to every full elementary cube in X a collection of full elementary cubes in X such that the union of the collection forms an acyclic cubical subset of X. Under the additional assumption of upper semicontinuity, such a map induces a map in homology.

An acyclic valued cubical map is represented as a blank seperated list of elements of the form

fec -> lfec

where fec is a full elementary cube, lfec is a braces enclosed, blank seperated list of full elementary cubes and each full elementary cube is represented as a parentheses enclosed, coma separated list of its minimal coordinates in each dimension.

The following example represents an acyclic valued cubical map of a cubical ring into itself which wraps the ring around itself twice. The file containting the example in the *.map format is available here.

(1,1) -> {(1,1) (2,1) (3,1)}
(1,2) -> {(1,1) (1,2) (1,3)}
(1,3) -> {(1,3) (2,3) (3,3)}
(2,1) -> {(3,1) (3,2) (3,3)}
(2,3) -> {(3,1) (3,2) (3,3)}
(3,1) -> {(1,3) (2,3) (3,3)}
(3,2) -> {(1,1) (1,2) (1,3)}
(3,3) -> {(1,1) (2,1) (3,1)}

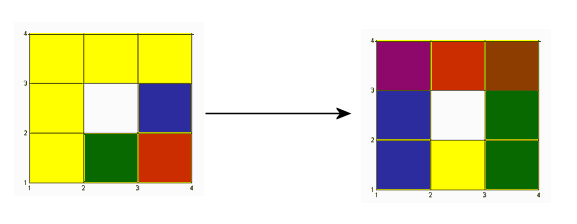
The following illustration shows the behaviour of the map on the blue red and green squares in the left cubical annulus. The blue cube is mapped to the collection of the two blue cubes and the violet cube in the right annulus. The red cube is mapped to the violet, red and brown cubes and the green cube is mapped to the brown and green cubes.