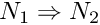 computations
computations
In the following examples we show how to use CAPD to integrate ODE along with variational equations to obtain not only image of a set but also normalized derivatives up to given order r with respect to initial conditions.
In general classes that we use have ICn prefix, which means that they rigorously (I) compute and store derivatives to given order (Cn).
Integration of ODE
We integrate a harmonic oscilator for a half of period with fixed time step. So we expect fist derivative to be 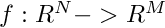 and the other derivatives to be equal 0.
and the other derivatives to be equal 0.
We need to include only one file
#include "capd/capdlib.h"
IMap f(
"var:x,y;fun:-y,x;",degree);
int numberOfSteps = 128;
double timeStep = PI/numberOfSteps;
solver.setStep(timeStep);
double radius = 0.1;
for(int i=0; i<numberOfSteps; ++i){
set.move(solver);
}
std::cout << "\n initial condition : " << v
<< "\n time of integration : " << numberOfSteps*timeStep
<<
"\n value : \n " <<
IVector(set)
<<
"\n C^1 derivative :\n" <<
IMatrix(set)
<< "\n all derivatives" << set.currentSet().toString();
The next example shows how to compute higher order derivatives with respect to initial condition with automatic step control along the trajectory.
Integration of ODE with automatic time step control (TSC)
In this example we changed the ODE and initial condition but in fact the only important difference is that instead of moving set "manually" we will use TimeMap class with automatic Time Step Control (TSC).
This class computes image of a given set after a given time.
Full source of this example
#include <iostream>
#include "capd/capdlib.h"
using namespace std;
const int degree = 3;
std::cout << "\n Michelson equation \n----------------------\n";
IMap f(
"par:c;var:x,y,z;fun:y,z,c^2-y-0.5*x*x;",degree);
double sizeOfSet = 0.005;
v[0]=0.0; v[1]=
interval(1.563-sizeOfSet, 1.563+sizeOfSet); v[2]=0.0;
timeMap(time, set);
cout << set.currentSet().toString();
return 0;
}
How to compute derivatives of order bigger than 3?
We need to specify the maximal degre of the vector field IMap in the last argument of the contructor.
const int degree = 5;
std::cout << "\n Michelson equation \n----------------------\n";
IMap f(
"par:c;var:x,y,z;fun:y,z,1-y-0.5*x*x;", degree);
Now we can use our types instead of built-in and the rest remains the same:
#include <iostream>
#include "capd/capdlib.h"
using namespace std;
const int degree = 5;
std::cout << "\n Michelson equation \n----------------------\n";
IMap f(
"par:c;var:x,y,z;fun:y,z,1-y-0.5*x*x;", degree);
double sizeOfSet = 0.005;
v[0]=0.0; v[1]=
interval(1.563-sizeOfSet, 1.563+sizeOfSet); v[2]=0.0;
timeMap(time, set);
cout << set.currentSet().toString();
return 0;
}
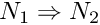 computations
computations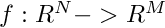 and the other derivatives to be equal 0.
and the other derivatives to be equal 0.