CAPD DynSys Library  5.2.0
Classes | Typedefs | Enumerations | Functions
capd::newton Namespace Reference

Classes

class  Krawczyk
 
class  Mapping
 General function for Newton or Krawczyk method f:R^n -> R^n. More...
 

Typedefs

typedef NewtonResult KrawczykResult
 

Enumerations

enum  NewtonResult { ResultUndefined = -2, TooManyIterations = -1, NoZeroes = 0, ZeroExists = 1 }
 Define results returned by Interval Newton Method. More...
 

Functions

template<typename FloatVector , typename MapType >
KrawczykResult KrawczykProof (const FloatVector &x, double size, MapType &F)
 
template<typename MapType >
KrawczykResult KrawczykProof (const typename MapType::VectorType &x0, const typename MapType::VectorType &X, MapType &F)
 
template<typename MapType >
MapType::VectorType KrawczykOperator (const typename MapType::VectorType &x0, const typename MapType::VectorType &X, MapType &F)
 
template<typename IntervalVector , typename IntervalMatrix >
void NewtonInfo (int, IntervalVector, IntervalVector, IntervalVector, IntervalMatrix, IntervalVector)
 Default function for writing details on Newton Proof. You can define your own specification to replace this default function. More...
 
template<typename FloatVector , typename MapType >
NewtonResult NewtonProof (FloatVector &x, double size, MapType &F)
 Rigorous existence proof of a zero of a given function F. More...
 
template<typename MapType >
NewtonResult NewtonProof (const typename MapType::VectorType &x0, const typename MapType::VectorType &X, MapType &F)
 Rigorous existence proof of a zero of a given function F. More...
 
template<typename MapType >
MapType::VectorType NewtonOperator (const typename MapType::VectorType &x0, const typename MapType::VectorType &X, MapType &F)
 Computes Newton operator. More...
 
template<typename FloatVector , typename MapType >
NewtonResult NewtonProof (const FloatVector &x, double size, MapType &F)
 
std::string resultToText (NewtonResult code)
 

Typedef Documentation

◆ KrawczykResult

typedef NewtonResult capd::newton::KrawczykResult

Enumeration Type Documentation

◆ NewtonResult

enum capd::newton::NewtonResult

Define results returned by Interval Newton Method.

Enumerator
ResultUndefined 
TooManyIterations 
NoZeroes 
ZeroExists 

Function Documentation

◆ KrawczykOperator()

template<typename MapType >
MapType::VectorType capd::newton::KrawczykOperator ( const typename MapType::VectorType &  x0,
const typename MapType::VectorType &  X,
MapType &  F 
)

◆ KrawczykProof() [1/2]

template<typename FloatVector , typename MapType >
KrawczykResult capd::newton::KrawczykProof ( const FloatVector &  x,
double  size,
MapType &  F 
)

◆ KrawczykProof() [2/2]

template<typename MapType >
KrawczykResult capd::newton::KrawczykProof ( const typename MapType::VectorType &  x0,
const typename MapType::VectorType &  X,
MapType &  F 
)

◆ NewtonInfo()

template<typename IntervalVector , typename IntervalMatrix >
void capd::newton::NewtonInfo ( int  ,
IntervalVector  ,
IntervalVector  ,
IntervalVector  ,
IntervalMatrix  ,
IntervalVector   
)
inline

Default function for writing details on Newton Proof. You can define your own specification to replace this default function.

◆ NewtonOperator()

template<typename MapType >
MapType::VectorType capd::newton::NewtonOperator ( const typename MapType::VectorType &  x0,
const typename MapType::VectorType &  X,
MapType &  F 
)

Computes Newton operator.

Parameters
[in]xapproximated zero of F, we assume that 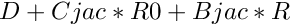$ x \in X $
[in]Xset X
[in]Fclass which can calculate value of the function F (by calling F(x)) and its derivative dF (by calling F[x])
Returns
N = x - (dF(X)^-1)*F(x)

◆ NewtonProof() [1/3]

template<typename FloatVector , typename MapType >
NewtonResult capd::newton::NewtonProof ( const FloatVector &  x,
double  size,
MapType &  F 
)

◆ NewtonProof() [2/3]

template<typename MapType >
NewtonResult capd::newton::NewtonProof ( const typename MapType::VectorType &  x0,
const typename MapType::VectorType &  X,
MapType &  F 
)

Rigorous existence proof of a zero of a given function F.

We compute rigorously Newton operator 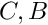$ N = x - (dF(X)^-1) F(x) $ and we check assumptions of the Interval Newton Method.

Parameters
[in]xapproximated zero of F, we assume that 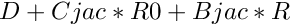$ x \in X $
[in]Xset X, in which we search for a zero of F
[in]Fclass which can calculate value of the function F and its derivative dF
Returns
NewtonResult constant: zeroExists = 1 - zero exists (K is subset of X), noZeroes = 0 - there is no zeros in the set X (intersection of K and X is empty), tooManyIterations = -1 - we can still take intersection of X and K, but we exceed maximal number of iteration undefined = -2 - X is subset of K,

◆ NewtonProof() [3/3]

template<typename FloatVector , typename MapType >
NewtonResult capd::newton::NewtonProof ( FloatVector &  x,
double  size,
MapType &  F 
)

Rigorous existence proof of a zero of a given function F.

We compute rigorously Newton operator 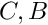$ N = x - (dF(X)^-1) F(x) $ and we check assumptions of the Interval Newton Method.

Parameters
[in]xapproximated zero of F,
[in]sizeradius of set X, ( $X = x + [-size, size]^n $ )
[in]Fclass which can calculate value of the function F (by calling F(x)) and its derivative dF (by calling F[x])
Returns
NewtonResult constant: zeroExists = 1 - zero exists (K is subset of X), noZeroes = 0 - there is no zeros in the set X (intersection of K and X is empty), tooManyIterations = -1 - we can still take intersection of X and K, but we exceed maximal number of iteration undefined = -2 - X is subset of K,

◆ resultToText()

std::string capd::newton::resultToText ( NewtonResult  code)
inline