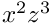CAPD DynSys Library  5.2.0
Main header files

Table of Contents

The library consists of a large number of template classes. For user convenience we provide three header files in which most important types are defined. All defined types are located in the capd namespace.

#include "capd/capdlib.h"
Note
File "capd/capdlib.h" provides classes for computation in double and long double precision and in interval arithmetics based on double type.
#include "capd/mpcapdlib.h"
Note
File "capd/mpcapdlib.h" provides classes for computation in multiple precision floating numbers and in interval arithmetics of arbitrary precision.

The last header file, "capd/fdcapdlib.h", defines types for computation in fixed at compile time dimension in user specified namespace. One can select many dimensions and locate them in different namespaces, like capd3, capd7.

This functionality is described in the program that proves the existence of 116 periodic solutions in the Lorenz system: see Multiple periodic solutions for the Lorenz system.

#include "capd/fdcapdlib.h"
Note
Fixing dimension at compile time usually speeds up computation.

Nonrigorous computation in double precision

Here is (not complete) list of types provided for a user in "capd/capdlib.h" file. All of these types have prefix D.

  • DVector - vector in Rn
  • DMatrix - matrix as an element of Rn×m
  • DHessian - data structure to store hessians of maps
  • DJet - data structure to store jets (coefficients in the Taylor series) of maps
  • DEuclNorm, DSumNorm, DMaxNorm - norms of vectors and matrices (operator norms).
  • DFunction - scalar valued function with vector arguments
  • DMap - a map from 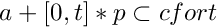$R^n \to R^m$. It can be used to define vector fields
  • DOdeSolver - solver to ODEs based on the (high order) Taylor method. It can integrate first order variational equations to ODEs.
  • DCnOdeSolver - solver to ODEs based on the (high order) Taylor method. It can integrate higher order variational equations to ODEs.
  • DTimeMap - computes solutions to ODEs over the time interval. It can integrate first order variational equations.
  • DCnTimeMap - computes solutions to ODEs over the time interval. It can integrate higher order variational equations.
  • DPoincareMap - computes Poincare maps and their first order derivatives.
  • DCnPoincareMap - computes Poincare maps and their higher order derivatives.
  • DNonlinearSection - most general Poincare section of the form $ \{x\in R^n : \alpha(x)=0\} $, where $ \alpha:R^n\to R$ is a smooth function
  • DAffineSection - Poincare section that is an affine hyperplane
  • DCoordinateSection - Poincare section that is of the form $ \{(x_1,\ldots,x_n)\in R^n : x_i = const\} $

Nonrigorous computation in long double precision

Here is (not complete) list of types provided for a user in "capd/capdlib.h" file. All of these types have prefix LD.

  • LDVector - vector in Rn
  • LDMatrix - matrix as an element of Rn×m
  • LDHessian - data structure to store hessians of maps
  • LDJet - data structure to store jets (coefficients in the Taylor series) of maps
  • LDEuclNorm, LDSumNorm, LDMaxNorm - norms of vectors and matrices (operator norms).
  • LDFunction - scalar valued function with vector arguments
  • LDMap - a map from 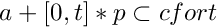$R^n \to R^m$. It can be used to define vector fields
  • LDOdeSolver - solver to ODEs based on the (high order) Taylor. It can integrate first order variational equations to ODEs.
  • LDCnOdeSolver - solver to ODEs based on the (high order) Taylor method. It can integrate higher order variational equations to ODEs.
  • LDTimeMap - computes solutions to ODEs over the time interval. It can integrate first order variational equations.
  • LDCnTimeMap - computes solutions to ODEs over the time interval. It can integrate higher order variational equations.
  • LDPoincareMap - computes Poincare maps and their first order derivatives.
  • LDCnPoincareMap - computes Poincare maps and their higher order derivatives.
  • LDNonlinearSection - most general Poincare section of the form $ \{x\in R^n : \alpha(x)=0\} $, where $ \alpha:R^n\to R$ is a smooth function
  • LDAffineSection - Poincare section that is an affine hyperplane
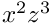
  • LDCoordinateSection - Poincare section that is of the form $ \{(x_1,\ldots,x_n)\in R^n : x_i = const\} $

Interval based computation in double precision

Here is (not complete) list of types provided for a user in "capd/capdlib.h" file. Most of these types have prefix I.

  • interval
  • IVector - interval vector in Rn
  • IMatrix - interval matrix as a subset of Rn×m
  • IHessian - data structure to store hessians of maps
  • IJet - data structure to store jets (coefficients in the Taylor series) of maps
  • IEuclNorm, ISumNorm, IMaxNorm - norms of vectors and matrices (operator norms).
  • IFunction - scalar valued function with vector arguments.
  • IMap - a map from 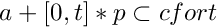$R^n \to R^m$. Can be used to define vector fields.
  • IOdeSolver - computes enclosures of trajectories for ODEs and associated variational equations. It can use (high order) Taylor method and/or (high order) implicit Hermite-Obreshkov method.
  • ICnOdeSolver - rigorous solver for ODEs and higher order variational equations.
  • C0Rect2Set, C0TripletonSet, C0HORect2Set, C0HOTripletonSet - various representations of subsets of 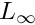$ R^n $ used in rigorous integration of ODEs by means of Taylor and Hermite-Obreshkov methods.
  • C1Rect2Set, C1HORect2Set, C2Rect2Set, CnRect2Set - various representations of jets of functions 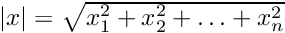$ R^n\to R^n $ used in rigorous integration of ODEs and (higher order) variational equations.
  • ITimeMap - computes enclosures of solutions to ODEs over the time interval. It can integrate first order variational equations.
  • ICnTimeMap - computes enclosures of solutions to ODEs over the time interval. It can integrate higher order variational equations.
  • IPoincareMap - computes rigorous bounds for Poincare maps and their first order derivatives.
  • ICnPoincareMap - computes rigorous bounds for Poincare maps and their higher order derivatives.
  • INonlinearSection - most general Poincare section of the form $ \{x\in R^n : \alpha(x)=0\} $, where $ \alpha:R^n\to R$ is a smooth function
  • IAffineSection - Poincare section that is an affine hyperplane
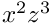
  • ICoordinateSection - Poincare section that is of the form $ \{(x_1,\ldots,x_n)\in R^n : x_i = const\} $

Nonrigorous computation in multiple precision

Here is (not complete) list of types provided for a user in "capd/mpcapdlib.h" file. All of these types have prefix Mp.

  • MpFloat - floating number of arbitrary precision
  • MpVector - vector in Rn
  • MpMatrix - matrix as an element of Rn×m
  • MpHessian - data structure to store hessians of maps
  • MpJet - data structure to store jets (coefficients in the Taylor series) of maps
  • MpEuclNorm, MpSumNorm, MpMaxNorm - norms of vectors and matrices (operator norms).
  • MpFunction - scalar valued function with vector arguments
  • MpMap - a map from 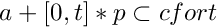$R^n \to R^m$. It can be used to define vector fields
  • MpOdeSolver - solver to ODEs based on the (high order) Taylor method. It can integrate first order variational equations to ODEs.
  • MpCnOdeSolver - solver to ODEs based on the (high order) Taylor method. It can integrate higher order variational equations to ODEs.
  • MpTimeMap - computes solutions to ODEs over the time interval. It can integrate first order variational equations.
  • MpCnTimeMap - computes solutions to ODEs over the time interval. It can integrate higher order variational equations.
  • MpPoincareMap - computes Poincare maps and their first order derivatives.
  • MpCnPoincareMap - computes Poincare maps and their higher order derivatives.
  • MpNonlinearSection - most general Poincare section of the form $ \{x\in R^n : \alpha(x)=0\} $, where $ \alpha:R^n\to R$ is a smooth function
  • MpAffineSection - Poincare section that is an affine hyperplane
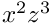
  • MpCoordinateSection - Poincare section that is of the form $ \{(x_1,\ldots,x_n)\in R^n : x_i = const\} $

Interval based computation in multiple precision

Here is (not complete) list of types provided for a user in "capd/mpcapdlib.h" file. These types have prefix Mp.

  • MpInterval
  • MpIVector - interval vector in Rn
  • MpIMatrix - interval matrix as a subset of Rn×m
  • MpIHessian - data structure to store hessians of maps
  • MpIJet - data structure to store jets (coefficients in the Taylor series) of maps
  • MpIEuclNorm, MpISumNorm, MpIMaxNorm - norms of vectors and matrices (operator norms).
  • MpIFunction - scalar valued function with vector arguments.
  • MpIMap - a map from 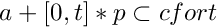$R^n \to R^m$. Can be used to define vector fields.
  • MpIOdeSolver - computes enclosures of trajectories for ODEs and associated variational equations. It can use (high order) Taylor method and/or (high order) implicit Hermite-Obreshkov method.
  • MpICnOdeSolver - rigorous solver for ODEs and higher order variational equations.
  • MpC0Rect2Set, MpC0TripletonSet, MpC0HORect2Set, MpC0HOTripletonSet - various representations of subsets of 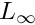$ R^n $ used in rigorous integration of ODEs by means of Taylor and Hermite-Obreshkov methods.
  • MpC1Rect2Set, MpC1HORect2Set, MpC2Rect2Set, MpCnRect2Set - various representations of jets of functions 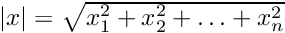$ R^n\to R^n $ used in rigorous integration of ODEs and (higher order) variational equations.
  • MpITimeMap - computes enclosures of solutions to ODEs over the time interval. It can integrate first order variational equations.
  • MpICnTimeMap - computes enclosures of solutions to ODEs over the time interval. It can integrate higher order variational equations.
  • MpIPoincareMap - computes rigorous bounds for Poincare maps and their first order derivatives.
  • MpICnPoincareMap - computes rigorous bounds for Poincare maps and their higher order derivatives.
  • MpINonlinearSection - most general Poincare section of the form $ \{x\in R^n : \alpha(x)=0\} $, where $ \alpha:R^n\to R$ is a smooth function
  • MpIAffineSection - Poincare section that is an affine hyperplane
  • MpICoordinateSection - Poincare section that is of the form $ \{(x_1,\ldots,x_n)\in R^n : x_i = const\} $